Passo 1
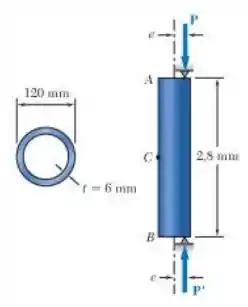
E ai gurizada tudo belezinha? O enunciado pede que a gente determine a) a força P para a qual a deflexão horizontal no ponto médio C seja de e (b) a tensão máxima correspondente na coluna
Temos então as seguintes dimensões:

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a) a força P para a qual a deflexão horizontal no ponto médio C seja de e (b) a tensão máxima correspondente na coluna
Temos então as seguintes dimensões: