Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 104
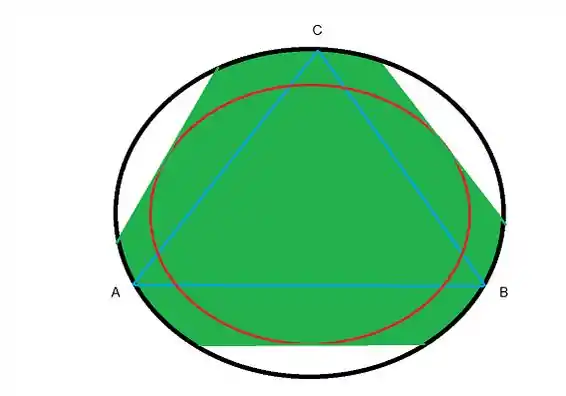
4.104. A mesa mostrada na figura pesa 120 N e tem um diâmetro de 1,2 m. É suportada por três pernas igualmente distribuídas nas extremidades. A carga vertical P de intensidade 400 N é aplicada no topo da mesa em D. Determine valor máximo de para a mesa não tombar. Mostre, num esboço, a área da mesa sobre a qual P possa seguir sem tombar a mesa.
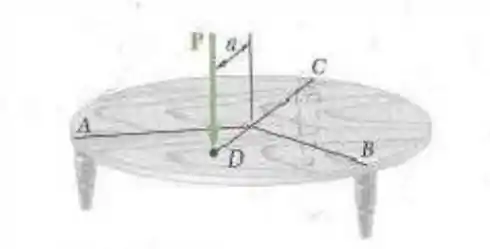
Passo 1
Vamos fazer um desenho com os pontos importantes da imagem
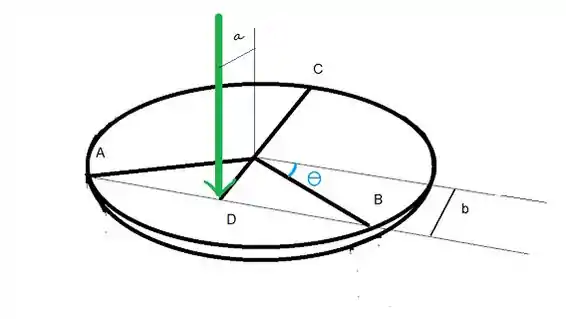
Bem, vamos determinar esse . Primeira coisa que precisamos saber é que dentro do circulo temos , como ele esta divido em três segmentos, entre um segmento e outro há . Então entre o segmento de C e B há , mas entre C e aquela linha mais fininha que colocamos acima de B há , logo .
Agora podemos determinar .
Como diâmetro é o raio é .
Passo 2
Como a mesa está parada, seu momento total é 0. Vamos calcular isso para o eixo
Esse W é a força peso que está agindo no centro da mesa.
Substituindo os valores
Então
Vamos deixar em função de
Passo 3
Bem, já que a mesa está em contato com o chão , então
Agora a gente pode isolar
Passo 4
Beleza, agora temos todas as forças de reação em função de , então podemos resolver o item (a), que diz que .
Passo 5
Agora só falta desenhar. As condições que temos é que , e a força P deve estar somente dentro das limitações perpendiculares geradas pelas pernas para a mesa não virar.
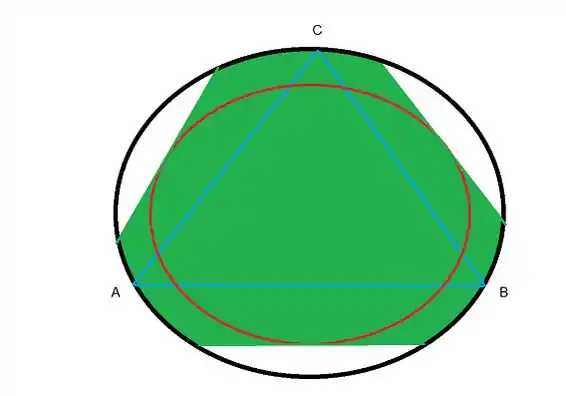
A linha vermelha representa .
A linha azul são as limitações geradas pelas pernas.
A área é Verde é a área que a força pode agir.
Resposta
