Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 84
84. Determine o maior peso do barril de óleo que a grua pode sustentar sem tombar. Além disso, quais são as reações verticais nas rodas lisas e para este caso? A grua tem peso de , com seu centro de gravidade localizado em .
Passo 1
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são três rodas lisas, segundo a tabela do capítulo , seção , esse tipo de conexão por roda só exerce uma força na direção vertical.
Vamos considerar um novo eixo para esse problema (que vai nos facilitar) que passa pelas duas rodas frontais da grua.
Abaixo temos um diagrama de corpo livre que vai nos ajudar a ver o que está acontecendo.
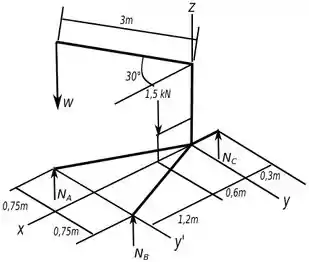
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.
O macete é sempre começar com as equações que te oferecem menos incógnitas.
Tomando isso, quando o barril tiver o maior peso possível a grua estará preste a tombar, então a força na roda , será nula, logo:
Vamos nos referir ao peso do barril como .
Passo 2
Agora vamos analisar a equação de equilíbrio referente ao momento em relação a .
Passo 3
Agora que temos essa informação a mais, vamos analisar a equação de equilíbrio referente ao momento em relação .
Agora analisando a equação de equilíbrio referente a força em relação ao eixo .
Pegando o que obtemos na primeira equação e jogando na segunda, ficamos com:
Logo: