Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 108

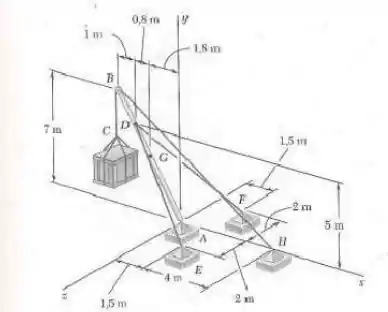
4.108. Um caixote de 2,400 N é suspenso por um cabo que passa pela polia B e é preso no suporte H. A lança AB de 800 N é suportada pela rótula em A e por dois cabos DE e DF. O centro de gravidade da lança é localizado em G. Determine (a) a tração nos cabos DE e DF, (b) a reação em A.

Passo 1

Vamos fazer o desenho disso

T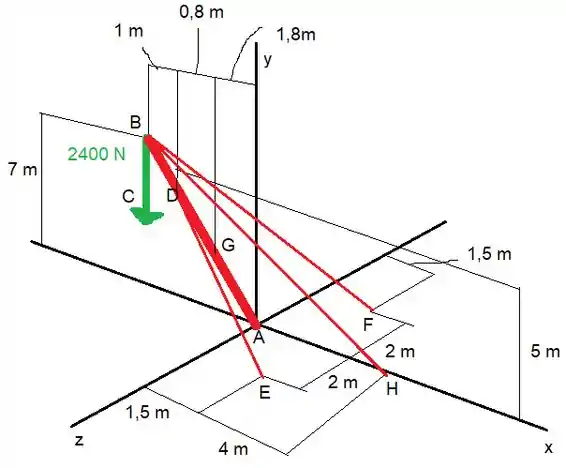

Bem, o que temos aqui são cinco variáveis T D E ,   T D F ,   A x ,   A y ,   A z e por sorte cinco equações de equilíbrio, então a gente vai conseguir. A lança é livre para girar no eixo AB, mas o equilíbrio se mantém e temos ∑ M A B = 0 .

Vamos começar já separando tudo que a gente precisa, que são os vetores e seus módulos

B H → = 9,1   î - 7   j ^   m

B H = 9,1 2 + 7 2 = 11,48   m

D E → = ( 4,1   î + 5   j ^

Passo 2

Agora a gente pode usar o esquema do momento

M A = ∑ r × F = 0

Então

M A = r A → × T A D → + T A E → + P → = 0

A gente não pode esquecer a força peso, jamais.

r A → = 2,4   k ^

P → = - 3,6   j ^

Agora a gente tem tudo

M A = 2,4   k ^ × T A D 2,6 - 0,8   i ^ + 0,6   j ^ - 2,4   k ^ + T B E 2,6 0,8   i ^ + 1,2   j ^ - 2,4   k ^ + - 3,6   j ^

Lembrando

i ^ × i ^ = j ^ × j ^ = k ^ × k ^ = 0

i ^ × j ^ = k ^

i ^ × k ^ = - j ^

j ^ × i ^ = - k ^

j ^ × k ^ = i ^

k ^ × i ^ = j ^

k ^ × j ^ = - i ^

M A = T A D 2,6 - 1,92   j ^ - 1,44   i ^ + T A E 2,8 1,92   j ^ - 2,88   i ^ + 8,64   î

M A = - T A D 2,6 1,44 - T A E 2,8 2,88 + 8,64 i ^ + - T A D 2,6 1,92 + T A E 2,8 1,92 j ^

E igualando os componentes à 0 temos

- T A D 2,6 1,44 - T A E 2,8 2,88 + 8,64 = 0   1

E

- T A D 2,6 1,92 + T A E 2,8 1,92 = 0   2

Passo 3

De (2) nós tiramos

T A D 2,6 1,92 = T A E 2,8 1,92

A gente pode cortar 1,92

T A D = T A E ⋅ 2,6 2,8 = 0,92857 T A E

Agora a gente substitui isso na equação (1)

0,92857 T A E 2,6 1,44 + T A E 2,8 2,88 = 8,64

T A E = 8,64 1,54286 = 5,6   k N

Então

T A D = 0,92857 ⋅ 2,8 = 5,2   k N

Passo 4

Agora a gente pode determinar a força de reação em C usando o somatório das forças em C.

Vamos começar em x

∑ F x = C x + T A D x + T A E x = 0

∑ F x = C x - 0,8 2,6 5,2 + 0,8 2,8 ⋅ 5,6 = 0

Então

C x = 0  

Agora em y

∑ F y = C y + T A D y + T A E y - P y = 0

∑ F y = C y + 0,6 2,6 5,2 + 1,2 2,8 ⋅ 5,6 - 3,6 = 0

Então

C y = 0  

E por fim em z

∑ F z = C z + T A D z + T A E z = 0

∑ F z = C z - 2,4 2,6 5,2 - 2,4 2,8 ⋅ 5,6 = 0

Então

C z = 2,4 2,6 5,2 + 2,4 2,8 ⋅ 5,6 = 9,6   k N

Logo

C → = 9,6   k ^   k N

Resposta

T A E = 5,6   k N

T A D = 5,2   k N

C → = 9,6   k ^   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mastro A B está no plano vertical y - z e é sustentado por uma rótula em B e por dois cabos em A . Calcule a força trativa em cada cabo devido à força de 20k N agindo no plano horizontal e aplicada
Uma barra uniforme de comprimento b e massa m está suspensa por suas extremidades por dois arames, cada um com comprimento b , a partir dos pontos A e B situados em um mesmo plano horizontal e separad
O guincho é usado para puxar a rede de peixe de 200k g para o píer. Determine a força compreensiva ao longo de cada uma das barras AB e CB e a tração no cabo do guincho DB. Considere que a força em ca
Determine a força em cada cabo para suportar a plataforma de 17,5k N ( ≈ 1750k g ). Considere d = 1,2m .
Determine a tração nos cabos para suportar a caixa de 100k g na posição de equilíbrio mostrada.