Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 101
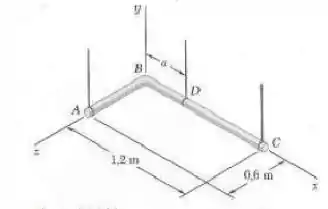
Dois tubos de aço e , cada qual com uma massa por unidade de comprimento de , são soldados juntos em e estão sustentados por três arames. Sabendo que , determine a tração em cada arame.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos calcular o peso de cada barra. Temos que:
Vamos aplicar a condição de equilíbrio:
Passo 2
Substituindo os vetores, temos que:
Resolvendo, teremos que:
Agora é só igualar os coeficientes correspondentes. Temos que:
Igualando os coeficientes de , temos que:
Logo:
Portanto:
Fazendo o somatório de forças em , temos:
Resposta
Exercícios de Livros Relacionados
Uma força P de 200N na manivela do carretel é requerida para enrolar o cabo subterrâneo a medida que ele sai do buraco. O tambor do carretel tem diâmetro de 1000m m . Para a posição horizontal da mani
O eixo, alavanca e manopla estão soldados e formam um único corpo rígido. Sua massa combinada é de 28k g , com centro de massa em G . O conjunto está montado sobre os mancais A e B e qualquer giro é e
Considere o conjunto do leme de um aeromodelo controlado por rádio. Para a posição a 15 ° mostrada na figura, a pressão atuando no lado esquerdo da área retangular do leme vale p = 4 10 - 5 N / m m 2
Cada uma das duas hastes da estrutura soldada tem massa de 50k g . Um arame desde C até D impede que a estrutura gire para fora do plano horizontal, em torno de um eixo que passa pelo mancal em B e pe
O poste rígido e as traves cruzadas do Prob. 2 / 105 estão mostrados novamente aqui. Determine as forças trativas T A E e T G F nos dois cabos de sustentação devidas à força trativa de 1,2k N no cabo