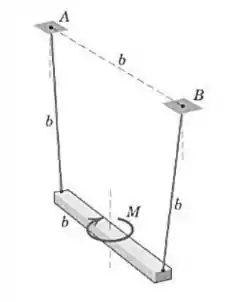
Uma barra uniforme de comprimento e massa está suspensa por suas extremidades por dois arames, cada um com comprimento , a partir dos pontos e situados em um mesmo plano horizontal e separados por uma distância . Um momento é aplicado à barra, fazendo com que ela gire em torno de um eixo vertical até a posição de equilíbrio mostrada. Deduza uma expressão para a altura até a qual a barra sobe a partir de sua posição original de equiíbrio, na qual ela está pendurada livremente sem nenhum momento aplicado. Qual valor de é necessário para erguer a barra ao valor máximo, ?
Passo 1
Imagine que você está de frente para a barra, com seu nariz apontando no sentido do comprimento dela. Nesse cao você enxerga o sistema como se fosse um pêndulo, e então a altura que a barra sobe (para ângulos pequenos) é a seguinte:
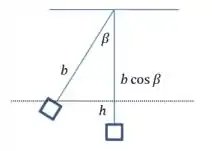
Ou seja, é uma função do ângulo beta, e é ele quem precisamos achar para resolver a questão.
Passo 2
Vamos definir alguns eixos e ângulos no desenho. Para simplificar vamos desenhar só as forças em uma das “metades” da barra, mas a mesma situação acontece do outro lado:
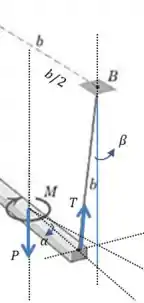
Vamos supor que o eixo seja esse eixo vertical que contém a força . Vamos analisar o equilíbrio das forças na direção dele (lembre-se de que existe outra força igual a essa do outro lado):
E vamos calcular também o momento em relação ao eixo (nesse caso o peso tem momento nulo, e a componente em da força também). Não esqueça de considerar o momento que é dado no enunciado (e que está no sentido horário):
O problema é que a componente de que é perpendicular ao eixo não é dada simplesmente por por :
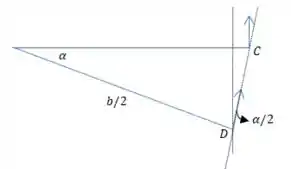
É preciso adicionar uma pequena correção pelo ângulo para encontrar a componente perpendicular à linha, então:
E o aparece no início da expressão porque esse mesmo momento é fornecido na outra extremidade da barra.
Então até agora temos o seguinte sistema:
Passo 3
Precisamos saber mais sobre o ângulo , mais especificamente sobre o ângulo . Olhe mais uma vez para o desenho que fizemos no passo :
Da mesma forma, podemos escrever a metade de se pegarmos a metade do ângulo apeas:
Isso ainda não resolve nosso problema. Existe alguma outra expressão conhecida para ? Sim, podemos escrever em função do ângulo (veja o primeiro desenho do passo ):
E então:
Passo 4
Vamos aproveitar essa inforação no nosso sistema:
E agora se dividirmos a primeira equação pela segunda:
E isolando :
E finalmente podemos voltar à fórmula do passo :
Como escrever quando só temos ?
E substituindo isso na fórmula:
Passo 5
E por último queremos considerar o caso em que a barra é erguida até o máximo, ou seja . Vamos substituir isso na fórmula:
E a única solução para essa equação é:
Resposta
A expressão é e o momento necessário para erguer a barra ao valor máximo é .