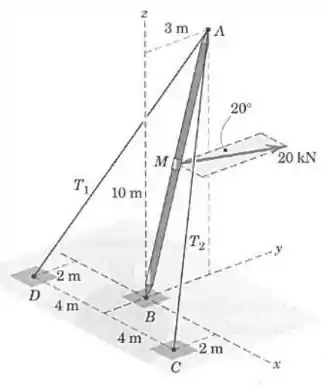
O mastro está no plano vertical e é sustentado por uma rótula em e por dois cabos em . Calcule a força trativa em cada cabo devido à força de agindo no plano horizontal e aplicada no ponto médio do mastro. Despreze o peso do mastro.

Para evitar a força exercida pela rótula em , vamos calcular o momento em relação ao eixo . Para isso vamos precisar dos vetores-posição que vão do eixo até os pontos onde cada uma das forças é aplicada.

Para as forças e temos:

E para a força (que atua no ponto médio do mastro) temos:

E então o momento em relação ao eixo é o seguinte:

Vamos começar resolvendo os três produtos vetoriais separadamente:

Mas como nós só vamos considerar as projeções sobre o eixo (afinal de contas temos que fazer o produto escalar de cada termo por ):

E essa é nossa primeira equação, precisamos encontrar mais uma.

Agora vamos considerar o momento em relação ao eixo . Mais uma vez a força em terá momento nulo, mas precisamos reescrever nossos vetores posição.

Dessa vez vamos fazer os vetores associados a e irem até o ponto (poderia ser qualquer ponto na linha de ação das forças):

E nem precisamos do produto vetorial para encontrar o momento gerado por em torno do eixo (sentido horário):

Falta então calcular o momento das forças e no eixo :

Começamos resolvendo essa soma de vetores:

E juntando tudo isso o momento em relação ao eixo fica:

Reescrevendo esse produto vetorial como o determinante de uma matriz:

Como no final só vamos pegar a componente podemos simplesmente só calcular essa parte do determinante:

E essa é nossa segunda equação!

Agora que temos duas equaçãoes e duas variáveis, podemos resolver o sistema para encontrar e :

Somando as duas equações:

E substituindo isso na primeira: