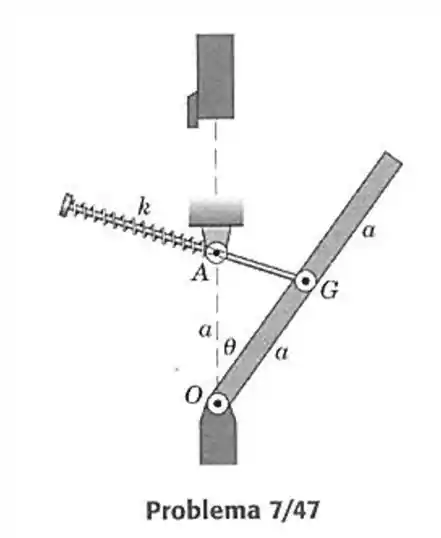
47- A seção transversal de um basculante articulado em relação ao eixo horizontal , de massa e com centro de massa em , está mostrada na figura. A medida que o basculante abre, a mola é comprimida pela haste articulada, que desliza através da bucha em . A mola não está comprimida quando o basculante está fechado. Mostre que o basculante ficará em equilíbrio para qualquer ângulo se a mola tiver uma rigidez apropriada.
Passo 1
Vamos desenhar o nosso sistema de forma que seja fácil ver as alturas e ângulos pertinentes.
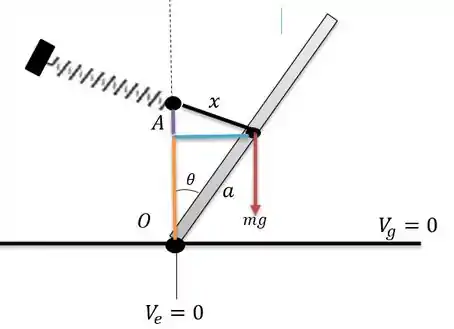
Onde o eixo da energia potencial gravitacional se encontra na base da estrutura e a energia potencial elástica seja em .
Para encontrar a energia potencial basta espelhar o centro de gravidade da barra na vertical de modo a encontrar sua altura de forma genérica.
Já que o centro de gravidade encontra-se acima do eixo nulo.
Passo 2
Agora para encontrar a energia potencial elástica, para isso podemos notar que na figura do passo 1 a deformação da molha é a distância cujo tamanho é a reta preta.
Mas para isso precisamos encontrar os catetos, formados pelas retas roxa e azul claro.
Quando espelhamos a metade da barra na vertical no passo 1 nós encontramos o tamanho da reta laranja e como a reta laranja somada com a reta roxa nos dá um tamanho de nós temos que:
E da mesma forma que espelhamos na vertical, logo na horizontal nós teremos o tamanho da reta azul, que é:
Agora fazendo Pitágoras nessas distâncias.
Explicitando :
Abrindo :
Como a energia elástica é dada por :
Poderemos substituir o que encontramos nela:
Logo a energia total do sistema será:
Passo 3
Se derivarmos em relação a a equação da energia nós teremos:
Se igualarmos a zero essa primeira derivada nós encontraremos o equilíbrio do sistema.
Como queremos que qualquer nos dê um sistema estável, vamos apenas considerar que ele é diferente de . Então para essa equação ser nós teremos somente uma constante igual a:
Se esse satisfazer essa condição podemos ter qualquer valor de para alcançar o equilíbrio.