Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 46

46- A alavanca está presa a uma das engrenagens montadas sobre mancais fixos, que estão ligadas por uma mola. A mola de rigidez k liga dois pinos, montados nas faces das engrenagens. Quando a alavanca está na posição vertical, θ = 0 e a força sobre a mola vale zero. Determine a força P necessária para manter o equilíbrio em um ângulo θ .

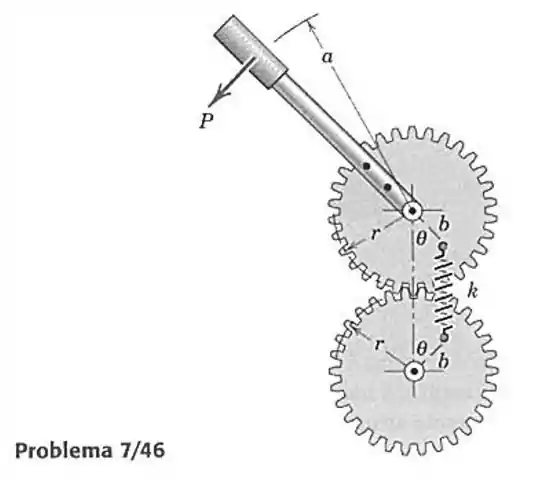
Passo 1

Esse exercício pode ser resolvido com trabalho virtual, da forma que:

δ V = δ V e

Uma vez que o momento imposto pela alavanca nos gerará energia potencial elástica e nada mais. Logo:

M d θ = K x   d x

P a d θ = K x   d x

Passo 2

Onde a variação da mola será calculada pela condição inicial e pelo trapézio abaixo.

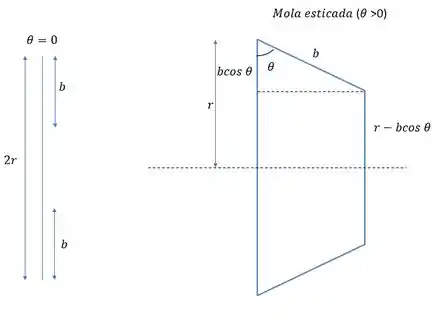
Onde o comprimento inicial da mola será dado por:

l 0 = 2 r - 2 b

E a mola esticada terá comprimento dado por:

l = 2 r - 2 b c o s   θ

Logo a deformação da mola será de

x = 2 r - 2 b c o s   θ - 2 r - 2 b c o s   θ = 2 b ( 1 - cos ⁡ θ )

Com sua variação valendo:

d x = 2 b s i n   θ d θ

Passo 3

Substituindo os valores de x e d x na equação do passo 1 teremos:

P a   d θ = k ( 2 b ( 1 - cos ⁡ θ ) 2 b s i n   θ d θ

Cortando d θ e passando a para o outro lado:

P = 4 b 2 k a sin ⁡ θ ( 1 - cos ⁡ θ )

Resposta

P = 4 b 2 k a sin ⁡ θ ( 1 - cos ⁡ θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 10.8, resolva o Problema 10.33.
Utilizando o método da seção 10.8, resolva o problema 10.39. Determine a estabilidade da estrutura. (Dica: A energia da mola é 1 2 k θ ² ) ²
Desprezando o peso dos blocos, determine a equação em termos de θ ,W ,lek que deve ser sitisfeita para que o sistema esteja em equilíbrio. Considere a mola indeformada quando a barra é horizontal.
Determine o valor do ângulo θ para equilíbrio se β = 30 ,P = Q = 400 N .
Determine o valor do ângulo θ para equilíbrio se β = 30 ,P = 100 NeQ = 25 N .