Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 100
Resolva o problema 10.99 se , e(a) e
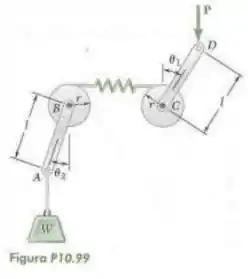
Passo 1
Fala aí galera, vamos para mais um problema de estática.
Sabemos que para encontrar a posição de equilíbrio, devemos encontrar a expressão da energia potencial e igualar sua derivada a 0. Logo, teremos que:
Vamos agora derivar a expressão:
Pegando a segunda derivada:
Para que o equilíbrio seja estável quando
Logo, substituindo os valores:
Resposta
Exercícios de Livros Relacionados
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .
Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 30 .
Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 6 0 .
A mola AB, de constante k , está indeformada quando θ = 0 , determine (a) os intervalos de θ para equilíbrio estável e (b) dois valores para equilíbrio tal que P é metade do limite superior encontrado
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .