Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 108
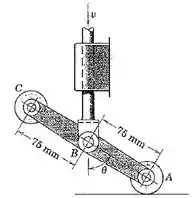
5/108) O dispositivo de comutação do Prob.5/85 é reapresentado aqui . Se a haste de controle vertical possui uma velocidade descendente de quando e se o cilindro está em contato contínuo com a superfície horizontal , determine pelo método da velocidade de para esse instante .
Passo 1
Então galera , analisando a figura do problema , temos que :
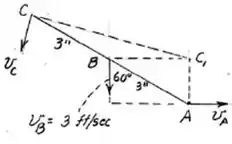
Agora para acharmos a velocidade do ponto precisaremos lembrar da relação :
Passo 2
Além disso , nós sabemos que a velocidade angular é a mesma para todo o sistema . Sendo assim :
Aplicando pitágoras achamos que a distância é dada por :
Logo , temos que :
Resposta
Exercícios de Livros Relacionados
Uma placa quadrada uniforme de 45 lb é suspensa de um pino localizado no ponto médio A de uma de suas bordas de 1,2 pés e é fixada a molas, cada uma com k constante: = 8 lb / in. se o canto B receber
Duas hastes uniformes, cada uma com massa em = 12 kg e comprimento L = 800 mm, são soldadas para formar o conjunto mostrado. Sabendo que a constante de cada mola é k = 500 N / m e que a extremidade A
Um disco uniforme de raio r = 250 mm está ligado em A a uma haste AB de 650 mm de massa desprezível, que pode girar livremente em um plano vertical em torno de B. Determine o período de pequenas oscil
Mostre que se o pêndulo composto do Problema 19.52 for suspenso de A em vez de 0, o período de oscilação é o mesmo de antes e o novo centro de oscilação está localizado em 0.
Um fio homogêneo dobrado para formar a figura mostrada é preso a um suporte de pino em A. Sabendo que r = 220 mm e que o Ponto B é empurrado para baixo 20 mm e liberado, determine a magnitude da veloc