Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 113

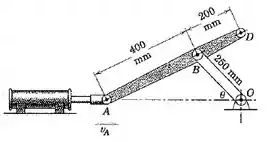
5/113) O cilindro hidráulico produz um movimento horizontal limitado do ponto A . Se v A = 4   m / s quando θ = 45 ° , determine o módulo da velocidade de D e da velocidade angular ω de A B D para essa posição .

Passo 1

Então pessoal , borá dar uma olhadana figura que mostra a situação do problema :

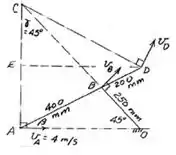
Aplicando a lei dos senos ao triângulo menor , obtemos que :

250 sen ⁡ β = 400 sen ⁡ 45 °

Logo ,

β = 26,2 °

Passo 2

Bom pessoal , agora que sabemos o valor de β , podemos calcular a distância entre os pontos da figura . Analisando a trigonometria do objeto , obtemos que :

A O - = 400 cos ⁡ 26,2 ° + 250 cos ⁡ 45 ° = 535,6   m m

A C - = A O - tan ⁡ 45 ° = 535,6   m m

E D - = 600 cos ⁡ 26,2 ° = 538,2   m m

C E - = 535,6 - 600 sen ⁡ 26,2 ° = 270,4   m m

Para acharmos a distância entre o ponto D e o centro instantâneo C , por sua vez , aplicamos Pitágoras :

C D - = 270,4 2 + 538,2 2 = 602,4   m m

Passo 3

Bom galera , nós sabemos que a velocidade angular de qualquer ponto com o centro instantâneo de velocidade é a mesma . Logo :

ω C D = ω C A

Ou seja ,

v D C D - = v A C A -

Portanto ,

v D = v A C D - C A - = 4 602,4 535,6 = 4,50   m / s

Para acharmos a velocidade angular da barra A B D , por sua vez , basta aplicarmos a relação :

ω A B D = ω = v A C A - = 4000 535,6 = 7,47   r a d / s

Resposta

v D = 4,50   m / s

ω A B D = 7,47   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/95) A barra A B possui uma velocidade angular no sentido anti-horário de 6r a d / s . Trace os vetores velocidade para os pontos A e G da barra e especifique os seus módulos se o centro instantâneo
5/108) O dispositivo de comutação do Prob.5/85 é reapresentado aqui . Se a haste de controle vertical possui uma velocidade descendente v de 0,9 m / s quando θ = 60 ° e se o cilindro A está em contato
5/109) A oscilação horizontal do êmbolo E acionado por uma mola é controlada por meio da variação da pressão do ar no cilindro pneumático horizontal F . Se o êmbolo possui uma velocidade para baixo v
5/100) O movimento da barra é controlado pelas trajetórias restritas de A e B . Se a velocidade angular da barra é de 2r a d / s no sentido anti-horátioquando a posição θ = 45 ° é ultrapassada , deter
5/103) As rodas vinculadas rolam sem deslizar sobre as placas A e B , que estão se movendo em sentidos opostos conforme mostrado . Se v A = 60m m / s para a direita e v B = 200m m / s para a esquerda