Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 109
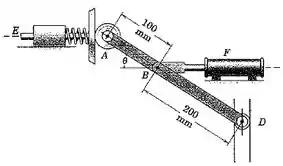
5/109) A oscilação horizontal do êmbolo acionado por uma mola é controlada por meio da variação da pressão do ar no cilindro pneumático horizontal . Se o êmbolo possui uma velocidade para baixo do rolete na guia vertical e encontre a velocidade angular de para essa posição .
Passo 1
Bom pessoal , analisando a figura do enunciado , obtemos que :
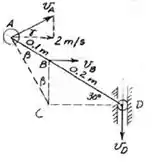
Agora vamos organizar os valores que já conhecemos . Sabemos que :
Além disso , como a soma dos ângulos internos de um triângulo é , temos que :
Logo , pela semelhança de triângulos , obtemos que :
Passo 2
Então galera , como podemos perceber pela figura do problema , a distância é dada por :
Para acharmos a velocidade do ponto , por sua vez , basta aplicarmos a relação :
Agora com essas duas grandezas definidas , a velocidade angular do sistema é facilmente obtida pela fórmula :
Passo 3
Bom galera , utilizando raciocínio análogo ao do passo anterior , temos que :
Além disso , como a velocidade angular é a mesma para todo o sistema , para acharmos a velocidade de basta aplicarmos a relação :