Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 5
Determine a distância até o centro de gravidade do elemento homogêneo.
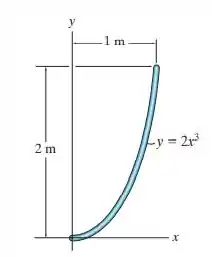
Passo 1
Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.
Para determinarmos a distância em do devemos utilizar na relação para o . Ela é dada por:
Onde é o comprimento do elemento. Primeiro, vamos determinar :
Passo 2
Agora, para determinarmos a posição do centro de massa, temos:
É isso, galera, Bora resolver mais questões pra ficar craque.
Resposta
Exercícios de Livros Relacionados
A figura mostra um corpo semelhante ao do Prob. 5/211, mas agora o corpo é uma casca fina com aberturas na base e no topo. Determine a altura h - de seu centro de massa, acima da base do sólido homogê
A barra uniforme de massa m está curvada em um quarto de arco circular, no plano vertical, e bascula livremente em A . A barra é mantida em posição pelo arame horizontal de O até B . Determine o módul
O corpo afilado tem uma seção transversal horizontal circular. Determine a altura h - de seu centro de massa, acima da base do sólido homogêneo.
Localize o centro de massa da casca esférica fina, que é formada cortando-se um oitavo de uma casca esférica completa.
Ache o ângulo θ que colocará o centro de massa do anel fino a uma distância r / 10 do centro do arco.