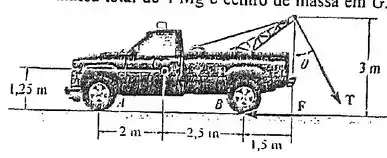
5.47. Determine a força de cabo mínima T e o ângulo crítico θ que fará com que o caminhão reboque comece a inclinar, ou seja, que a reação normal em A seja zero. Assuma que o caminhão esteja freado e não deslizará em B. O caminhão tem massa total de e centro de massa em G.
Passo 1
Fala, querido! Queremos saber mínimo e quando . Vamos fazer um DCL. A gente vai representar esse carro com o guindaste por um retângulo:
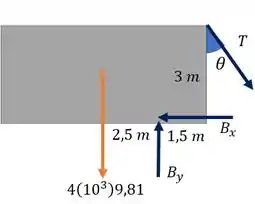
Aí a gente vai usar as equações de equilíbrio da estática para achar o que ele pede.
Passo 2
Beleza, como o sistema está estático, podemos dizer que
Repara que tanto a componente horizontal de quanto a vertical vão causar momento em . Então ambas aparecem aqui. Vamos considerar o sentido anti-horário positivo.
Logo
Passo 3
Cara, encontramos ali em cima uma expressão para a tração em função do ângulo que faz com que o caminhão tombe. No entanto, o enunciado pediu para a gente encontrar o menor valor de tração que faria isso.
Como temos uma função e queremos o valor mínimo dessa função, é só lembrarmos de cálculo 1 que para encontrarmos o máximo ou mínimo de uma função, só precisamos derivar e igualar a zero.
Então a gente precisa achar que satisfaz essa equação. Repara que o enunciado o chama de crítico e é exatamente por isso! Ele é o que zera nossa derivada. Ou seja, o ponto crítico de .
Vamos calcular então:
E igualar a zero:
Logo podemos concluir que
Passo 4
Agora que sabemos θ, vamos calcular T