Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 53
5.53. Determine o ângulo em que a ligação ABC se mantém em equilíbrio se o membro BD se mover para a direita. As molas estão originalmente descarregadas quando . Cada mola possui a rigidez mostrada. As molas permanecem na horizontal, já que estão conectadas a guias de rolos.
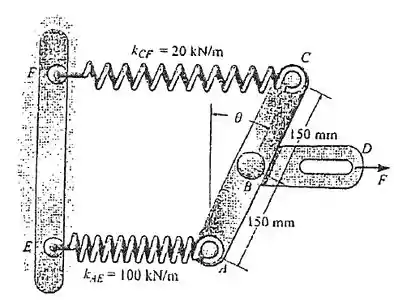
Passo 1
Falaaa! Então, a situação aqui é que uma força causa esse deslocamento em . Só que temos forças nas extremidades dessa barrinha. Essas forças e a força que causou o deslocamento ficam em equilíbrio.
Como a gente tem na verdade forças elásticas nas extremidades, para descobrir esse ângulo , precisamos descobrir o quanto essas molas ficam deformadas no equilíbrio com a força . Ok?
Bora começar com o DCL:
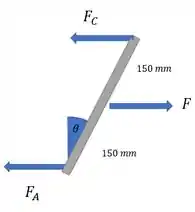
Passo 2
Beleza, como o sistema está estático, podemos dizer que
Adotando o sentido anti-horário como positivo e percebendo que o braço de alavanca das forças é a projeção de no eixo vertical:
Daí tiramos que
E do somatório de forças na horizontal:
Passo 3
Agora pensa comigo. Como essas forças são elásticas, elas podem ser escritas como
Daí a gente consegue achar expressões para e , as deformações das molas:
Então
Para :
Se liga, que esses valores estão em metros.
Passo 4
Vamos usar semelhança de triângulos para achar :
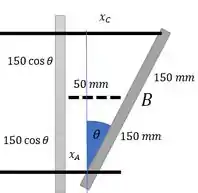
Usando as medidas em metros:
Isolando
Passo 5
E finalmente, olhando o triângulo que a gente fez:
E