Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 39

5.39. A mola CD permanece na posição horizontal o tempo todo devido ao rodízio em D. Se a mola está descarregada quando θ = 0 e a rigidez é k = 1,5 k N m , determine o menor ângulo θ para o equilíbrio e as componentes horizontal e vertical da reação no pino A

Passo 1

Beleza, a gente pode começar determinando a força da mola, vamos chamar essa força de F k , deixa que eu te lembro que podemos calcular essa força assim

F k = k ⋅ x

E aí podemos determinar x, usando esse triângulo

x = 0,6 ⋅ sin ⁡ θ

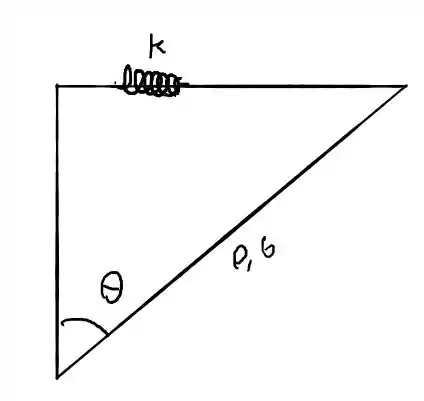
Então

F k = 1500 ⋅ 0,6 ⋅ sin ⁡ θ = 900 ⋅ sin ⁡ θ

Passo 2

Mas ainda não determinamos a constante da mola k , vamos usar o fato de que o sistema está em equilíbrio e então dizer que a somatória do momento em A é 0.

M A = 0

M A = 900 ⋅ sin ⁡ θ ⋅ cos ⁡ θ ⋅ 0,6 - 300 ⋅ sin ⁡ θ ⋅ 0,6 ) - 300 ⋅ c o s ⁡ θ ⋅ 0,45 = 0

540 ⋅ sin ⁡ θ ⋅ cos ⁡ θ - 180 ⋅ sin ⁡ θ - 135 ⋅ cos ⁡ θ = 0

Isso nos dá que

θ = 23,1 °

Passo 3

Agora vamos usar a equação de equilíbrio ao longo do eixo y para determinar a componente vertical da força.

F R y = 0

F R y = A y - 300 = 0

A y = 300   N

Passo 4

Agora só falta a componente horizontal. Vamos usar a equação de equilíbrio ao longo do eixo x

F R x = 0

F R x = A x - 900 ⋅ sin ⁡ 23,1 ° = 0

A x = 352,8   N

Resposta

A x = 352,8   N

A y = 300   N

θ = 23,1 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

72. Determine as reações em A e B quando β = 30 ° .
75. O elemento A B C é sustentado por um pinoe e um suporte em B e por uma corda inextensível presa em A e C passando por uma polia sem atrito em D . Pode-se supor que a tração seja a mesma na porção
76. O elemento A B C é sustentado por um pinoe e um suporte em B e por uma corda inextensível presa em A e C passando por uma polia sem atrito em D . Pode-se supor que a tração seja a mesma na porção
77. A haste A B é suportado por um pino e um suporte em A e apoia sem atrito numa cavilha em C . Determine as reações em A e C quando a força vertical de 170N é aplicada em B .
78. Resolva o problema 4.77 considerando que a força de 170N aplicada em B é horizontal e direcionada para a esquerda: