Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 49
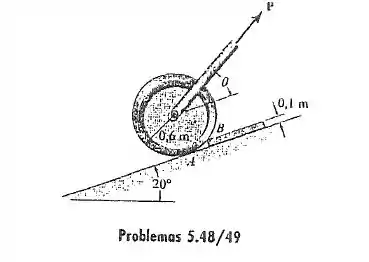
5.49. Determine a intensidade e direção da força P mínima necessária para puxar o cilindro de pelo degrau liso.
Passo 1
Cara, ele pediu para a gente achar mínimo e correspondente que faça mover esse cilindro pelo degrau liso. O melhor é sempre começar pelo DCL para entender o que está havendo:
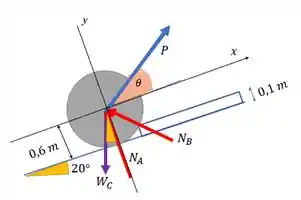
Esse retângulo azul é o degrau, tá? Temos o peso do cilindro para baixo que vale
Temos as forças normais de contato em e . E temos a força orientada de .
Só que repara uma coisa, na eminência do movimento, quando o cilindro está quase saindo do lugar, a normal em zera, aí fica só como normal.
Percebe que a gente vai usar esse sistema de eixos inclinados, para facilitar as contas, ou seja na direção do plano e perpendicular ao plano.
Como está tudo em equilíbrio, podemos usar as equações de equilíbrio de forças e momentos.
Bora lá!
Passo 2
Agora podemos usar o fato que o momento total é 0 e fazer o somatório de momentos no ponto . Aí a gente pode ignorar e achar .
Vamos decompor nossas forças em relação a e para achar os braços de alavanca certinho.
Mas antes a gente precisa achar o braço de alavanca da componente de do eixo em relação a , porque isso não tá claro na figura. Vamos reunir as informações que temos
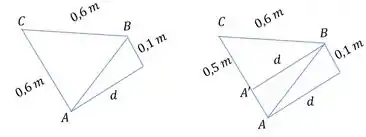
No nosso desenho é o centro do cilindro. Percebe que ali a gente tem um triângulo retângulo. Aí podemos fazer:
Isolando :
Passo 3
Agora sim, a gente a parte para o somatório de momentos
Daí a gente tira uma expressão para :
Passo 4
Agora a gente vai lembrar láaa de cálculo 1. Quando a gente queria achar onde uma função era mínima, nós derivávamos a função e igualávamos essa derivada a zero certo? Aí a gente isolava nossa variável e descobria onde a função era mínima.
Temos aqui uma função para usando a variável . Cara, ele pede para mínimo, lembra? Então o que vamos fazer para acharmos o ângulo em que é mínimo vai ser derivar em função de e igualar a 0.
Repare que para isso tudo ser 0 basta que
Então vamos isolar
Uhul! Achamos !
Passo 5
Agora basta encontrar mínimo substituindo lá na função que achamos de