O cone homogêneo tem uma cavidade cônica cortada, conforme a figura. Determine a profundidade d da cavidade em termos de h de modo que o cone se equilibre sobre o pivô e permaneça em equilíbrio indiferente.
Passo 1
Diagrama do corpo livre:
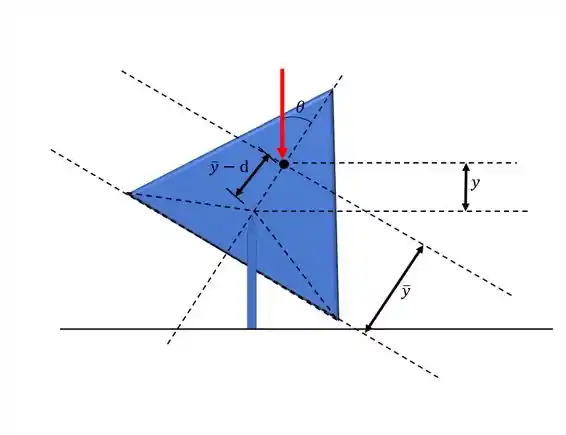
Passo 2
Começamos escrevendo a equação do centro de gravidade do cone com respeito à base:
H é altura do cone, de é a altura interna do cone. é o centro de gravidade do cone.
Então, podemos escrever que:
Passo 3
Agora podemos escrever a equação da função da energia potencial para o sistema:
Passo 4
Para encontrar a posição de equilíbrio, precisamos encontrar a primeira derivada da expressão da energia potencial:
Passo 5
Para analisar o equilíbrio, devemos tomar a segunda derivada:
Portanto a profundidade do cone deve ser para que haja equilíbrio indiferente