Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 20

Uma força axial é necessária para remover a polia de seu eixo. Que força deve ser exercida na alça de cada uma das duas alavancas? O atrito nos pontos de contato e é suficiente para evitar o escorregamento; o atrito nos pontos de contato da polia e é insignificante.

Passo 1

Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar a força que deve ser aplicada na extremidade de cada uma das duas alavancas para remover a polia de seu eixo. A melhor forma de entender um problema é começando pelo seu diagrama de corpo livre. É importante lembrar que tudo que a gente fizer para uma alavanca serve para a outra, uma vez que elas são simétricas e espelhadas. Sendo assim, vamos trabalhar separadamente com a barra responsável por aplicar metade da força axial necessária ().

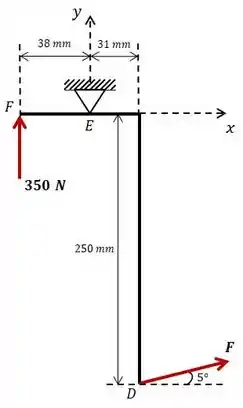
Não colocamos as reações no ponto de contato , porque vamos calcular o momento em torno desse ponto e o momento produzido por qualquer força ao redor do ponto de aplicação dela é nulo.

Passo 2

Até aqui só introdução, vamos partir para os cálculos! Primeiramente, vamos decompor nos eixos e :

Para os nossos cálculos, vamos adotar que as forças são positivas quando estiverem nos sentidos positivos dos eixos (apontando para a direita em e para cima em ). Já os momentos serão considerados positivos quando estiverem no sentido anti-horário e negativos no sentido horário.

Nosso problema é denominado Categoria 4 segundo a classificação do quadro da Fig. 3/3. Isso significa que precisaríamos de duas equações de forças (eixos e ) e uma de momento (eixo ) para resolver o sistema de incógnitas. Por outro lado, temos apenas uma incógnita , que no caso pode ser encontrada apenas pela equação de equilíbrio do momento em torno de :