Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 19
Determine a massa mínima do cilindro necessária para causar perda de contato em .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a massa mínima () que o cilindro deve ter para que a barra perca o contato no ponto . Esse exercício é um pouco maior, mas não vamos desanimar hein? Bora lá!
Vamos começar analisando o cilindro separadamente:
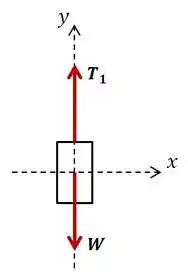
O peso do cilindro é dado por:
Fazendo o somatório de forças em para o cilindro, podemos encontrar a tensão no cabo de sustentação:
Agora vamos fazer o mesmo isolando a polia:
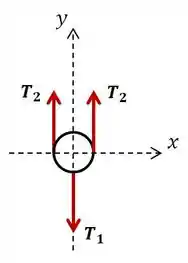
Passo 2
Show de bola! Com isso, já podemos analisar a barra separadamente. Nela estão atuando as reações no pivô , a reação normal em e a tensão do cabo 2. Para facilitar os cálculos, vamos dividir a barra em duas: e . Assim não temos que descobrir o centro de massa da barra .
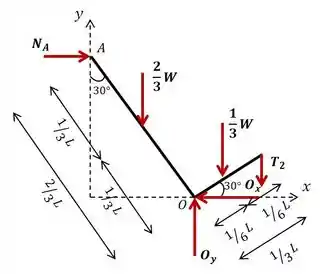
Além de , ainda nos restam três incógnitas: , e , onde a que realmente nos interessa é para determinar . O pulo do gato é escolher qual equação de equilíbrio usar nesse caso. Como as reações e estão sendo aplicadas exatamente neste ponto, elas não produzem momento ao redor dele, nos restando apenas como incógnita.
Passo 3
Calma que tá acabando hehe! Até aqui, a normal está em função de . O enunciado nos pediu para determinar a massa mínima necessária para que a barra perdesse o contato no ponto . O contato só existe se for de compressão (positiva), ou seja, para que seja de tensão:
Então a massa mínima para quebrar esse contato em é:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 