Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 49
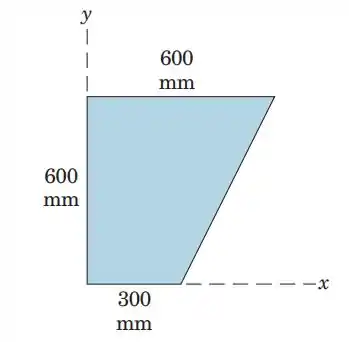
5.49. Determine the coordinates of the centroid of the trapezoidal area shown.
Passo 1
Para encontrar as coordenadas do centroide podemos usar as equações
Mas esse problema aqui vai simplificar as coisas para a gente, porque a densidade é homogênea. Então ficamos com
Passo 2
Beleza, vamos fragmentar o problema em duas figuras mais fáceis de resolver
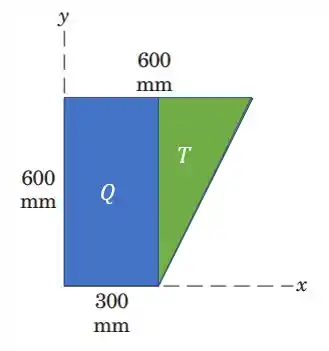
Vamos começar com o retângulo .
E
Agora temos as coordenadas do centroide do retângulo.
E a área fica o seguinte
Passo 3
Agora vamos para o triângulo. Para ficar mais fácil resolver vamos mudar o centro de coordenadas.
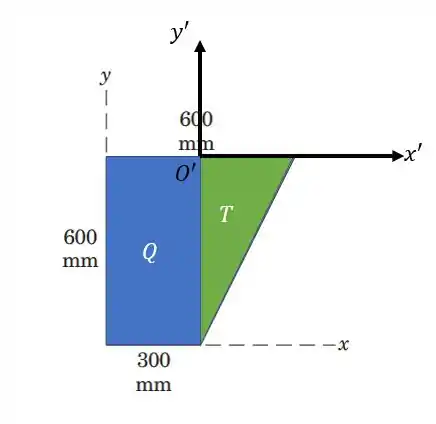
A equação para as novas coordenadas fica
E a coordenada da nova origem é
Agora vamos determinar o centroide do triângulo nessas coordenadas
Vamos passar isso para o sistema de coordenadas originais
E a área do triângulo é:
Passo 4
Agora vamos calcular o centroide da figura toda.
Isso fica
Substituindo os valores
E para
Isso fica
Então