Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 1
Localize o centroide da área plana mostrada
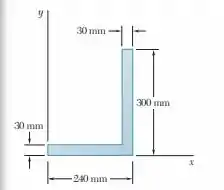
Passo 1
Fala ai galerinha, encoooxxxxta que eu explicoooo!!
Vamos considerar a área plana nas áreas simples, conforme mostrado no diagrama a seguir:
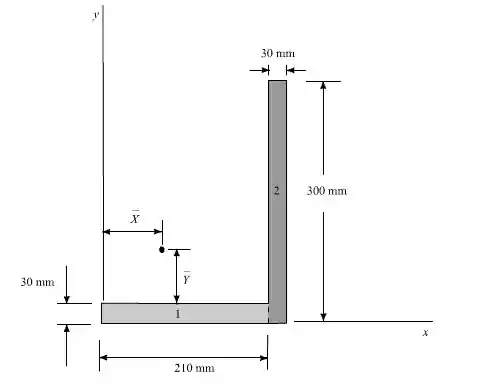
Passo 2
Vamos calcular a área da seção 1 (Retângulo ).
Onde, a largura e a profundidade da seção 1 são .
Substituiremos
Vamos calcular a distância do centroide horizontal da seção 1:
Substituindo :
Vamos calcular a distância do centroide vertical da seção 1:
Substituindo
Passo 3
Vamos calcular a área da seção 2 (Retângulo ).
Onde, a largura e a profundidade da seção 2 são .
Substituiremos
Vamos calcular a distância do centroide horizontal da seção 2:
Substituindo :
Vamos calcular a distância do centroide vertical da seção 2:
Substituindo
Passo 4
Iremos calcular agora a distância do centroide horizontal da área total usando a seguinte relação
Substituindo os valores que obtivemos nos passos anteriores:
Passo 5
Iremos calcular agora a distância do centroide vertical da área total usando a seguinte relação
Substituindo os valores que obtivemos nos passos anteriores:
Resposta
Portanto, as coordenadas do centroide da área do plano são respectivamente.