Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 2
Determine o centroide das áreas planas a seguir.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos subtrair as superfícies conforme a figura abaixo:
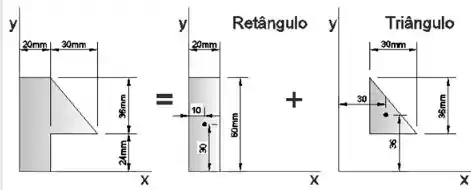
Conforme eixo de coordenadas, amnos os retângulos têm coordenadas positivas. Calculando-se os momentos estáticos das superfícies indicadas anteriormente, conforme equação compacta a seguir:
Passo 2
Agora, vamos construir a tabela para podermos definir o centroide da figura:
Passo 3
Com as informações obtidas na tabela anterior, podemos definir o centroide da figura, em que:
Substituindo os valores da tabela, temos que:
E:
Resposta
Exercícios de Livros Relacionados
With your pencil, make a dot on the position of your best visual estimate of the centroid of the triangular area. Check the position of your estimate by referring to the results of Sample Problem 5/2
Determine the y-coordinate of the centroid of the shaded area. Check your result for the special case a = 0.
Determine the x- and y-coordinates of the centroid of the shaded area.
5.29. Determine the y-coordinate of the centroid of the shaded area.
5.35. Determine the x-coordinate of the mass center of the portion of the spherical shell of uniform but small thickness.