Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 55

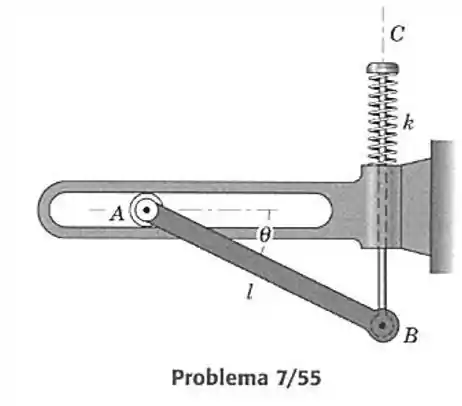
55- A conexão uniforme A B tem massa m e sua extremidade esquerda A desliza livremente no rasgo horizontal fixo. A extremidade B está presa ao êmbolo vertical, que comprime a mola quando B está presa ao êmbolo vertical, que comprime a mola quando B desce. A mola estaria sem compressão na posição θ = 0 . Determine o ângulo θ para o equilíbrio(diferente daquele para a posição impossível, correspondente a θ = 90 ° ) e indique a condição que garantirá a estabilidade.

Passo 1

Vamos fazer o desenho dessa conexão antes de depois da barra rotacionar um ângulo θ .

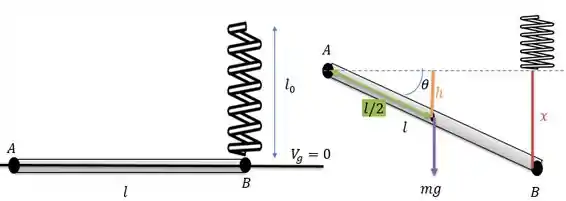
Inicialmente quando θ = 0 a barra encontra-se no eixo nulo de energia potencial gravitacional e amola encontra-se com seu comprimento natural l 0 quando abaixa-se na vertical o ponto B surge um ângulo θ entre a barra e a horizontal, de modo que agora o centro de massa da barra encontra-se abaixo do eixo nulo se tornando negativa, e a mola é comprimida com o mesmo tamanho da reta vermelha na figura. De modo que.

sin ⁡ θ = x l → x = l s i n   θ

E o centro de gravidade (que encontra-se no meio da barra) encontra-se agora em uma altura igual a:

sin ⁡ θ = h l 2 = h = l 2 sin ⁡ θ

Logo a energia total do sistema agora valerá:

V = V g + V e = - m g h + 1 2 k x 2 = - m g l 2 sin ⁡ θ + k 2 l 2 sin 2 ⁡ θ

Passo 2

Derivando a equação da energia uma vez nós conseguiremos encontrar a posição de equilíbrio do sistema.

d V d θ = - m g l 2 cos ⁡ θ + k l 2 sin ⁡ θ cos ⁡ θ

Igualando essa equação a zero nós encontraremos a condição de equilíbrio do sistema:

cos ⁡ θ ( - m g l 2 + k l 2 sin ⁡ θ ) = 0

Logo para essa equação se verdadeira ou cos ⁡ θ = 0 o que faz com que θ = π / 2 o que é impossível, o próprio enunciado nos fala.

Ou - m g l 2 + k l 2 sin ⁡ θ = 0 , o que faz com que:

k l 2 sin ⁡ θ = m g l 2

Isolando sin ⁡ θ nós teremos:

sin ⁡ θ = m g 2 k l

Como condição de equilíbrio.

Passo 3

Como sin ⁡ 2 θ = 2 cos ⁡ θ sin ⁡ θ nós poderemos escrever a equação da seguinte maneira também:

d V d θ = k l 2 2 sin ⁡ 2 θ - m g l 2 cos ⁡ θ

Derivando então essa última derivada nós conseguimos encontrar as condições de estabilidade do sistema.

d 2 V d θ 2 = k l 2 cos ⁡ 2 θ + m g l 2 sin ⁡ θ

Das relações trigonométricas:

cos 2 ⁡ x + sin 2 ⁡ x = 1

E

cos 2 ⁡ x - sin 2 ⁡ x = cos ⁡ 2 x

Conseguimos chegar em:

1 - 2 sin 2 ⁡ x = cos ⁡ 2 x

Agora substituindo o valor de equilíbrio que encontramos na equação da derivada segunda e fazendo ela ser estável, ou seja ela ser maior que zero, nós teremos:

k l 2 [ 1 - 2 sin 2 ⁡ θ ] + m g l 2 s i n θ > 0

Posição de equilíbrio: s i n θ = m g 2 k l

k l 2 1 - 2 m g 2 k l 2 + m g l 2 × m g 2 k l > 0

k l 2 1 - 2 m 2 g 2 4 k 2 l 2 + m 2 g 2 4 k > 0

k l 2 - m 2 g 2 2 k + m 2 g 2 4 k > 0

4 k 2 l 2 - 2 m 2 g 2 + m 2 g 2 > 0

4 k 2 l 2 > m 2 g 2

Tirando a raiz dos dois lados:

2 k l > m g

k > m g 2 l

Que é a condição necessária para o sistema ser estável.

Resposta

Equilíbrio em sin ⁡ θ = m g 2 k l

Estabilidade: k > m g 2 l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma semiesfera homogênea de raio r é posicionado em uma inclinação como mostra a figura. Considerando que o atrito é suficiente para evitar o escorregamento entre a semiesfera e a inclinação, determin
Duas barras uniformes idênticas, cada qual de massa m e comprimento l , estão unidas a engrenagens, tal como mostra a figura. Para o intervalo 0 ≤ θ ≤ 180 ° , determine as posições de equilíbrio do si
Mostre quer o equilíbrio é neutro no problema 10.6.
Mostre quer o equilíbrio é neutro no problema 10.1.
Usando o método da seção 10.8, resolva o probelma 10.35.