Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 110

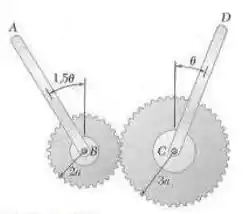
Duas barras uniformes idênticas, cada qual de massa m e comprimento l , estão unidas a engrenagens, tal como mostra a figura. Para o intervalo 0 ≤ θ ≤ 180 ° , determine as posições de equilíbrio do sistema e determine em cada caso se o equilíbrio é estável, instável ou neutro.

Passo 1

Questão um pouco grande, mas nem tão complicada! Vamos primeiro passar para a geometria do problema! Da energia potencial:

V = W   1 2 cos ⁡ 1.5 θ + W 1 2 c o s θ

d V d θ   = W l 2 - 1.5 sin ⁡ 1.5 θ + W l 2   - s e n   θ = - W l 2 ( 1.5 sin ⁡ 1.5 θ + sin ⁡ θ )

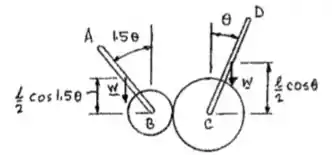
Passo 2

Logo, vamos derivar duas vezes a nossa expressão para o equilíbrio!

d V d x = 8 2 x 3 - 4 2 3 - 20  

d 2 V d θ 2 = - W l 2 ( 2.25 cos ⁡ 1.5 θ + cos ⁡ θ )

d V d θ = 0 ;

1.5 sin ⁡ 1.5   θ + sin ⁡ θ = 0

Passo 3

Agora vamos analisar as soluções. Uma solução, por inspeção, é a que θ = 0 , e a segunda expressão menor de 180   °

θ = 2,4042   r a d = 137,8   °

Agora,

d 2 V d θ 2 = - W l 2 ( 2.25 cos ⁡ 1.5 θ + cos ⁡ θ )

Para a solução de θ = 0 .

d 2 V d θ 2 = - W l 2 2.25 cos ⁡ 0 + cos ⁡ 0 =   - W l 2 ( 3.25 )

E essa solução é instável, pois é menor que 0!

Temos que para θ = 137.8   °

d 2 V d θ 2 = - W l 2 2.25 cos ⁡ 1.5 ⋅ 137.8   ° + cos ⁡ 137.8   ° = W l 2 2.75

E essa solução é estável, pois é menor que 0! Portanto o ângulo que a gente procura é de θ = 137.8   ° .

Resposta

θ = 137.8   °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola está livre quando θ = 45 º ºe tem uma rigidez k = 20k N / m . Determine o ângulo θ para o equilíbrio se cada um dos cilindros pesa 250 N. Despreze o peso dos membros.
Uma mesa de servir uniforme com 5 kg é apoiada em cada lado por pares de ligações idênticas , AB e CD, e molas CE. Se a tigela tem uma massa de 1 kg, determine o ângulo θ onde a mesa está em equilíbri
O cone homogêneo tem uma cavidade cônica cortada, conforme a figura. Determine a profundidade d da cavidade em termos de h de modo que o cone se equilibre sobre o pivô e permaneça em equilíbrio indife
A montagem mostrada consiste em um bloco semicilíndrico e retangular. Se o bloco pesa 40 N e o semicilindro 10 N, investigue a estabilidade quando a montagem estiver apoiada na posição de equilíbrio.
Um bloco homogêneo repousa no topo da superfície cilíndrica. Derive a relação entre o raio do cilindro, r, e a dimensão do bloco b, para o equilíbrio estável. Dica: estabeleça a função energia potenci