Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 51
5.50. Determine the y-coordinate of the centroid of the shaded area.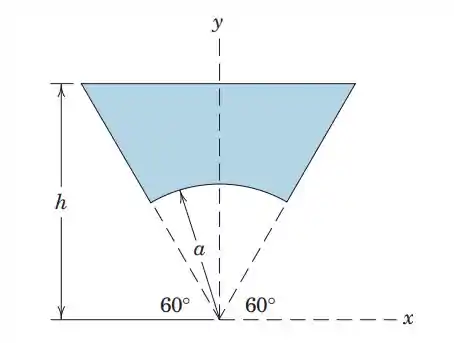 
Passo 1
Vamos achar outro centroide, mas agora é só para o eixo .
Beleza, vamos fragmentar o problema em três figuras mais fáceis de resolver
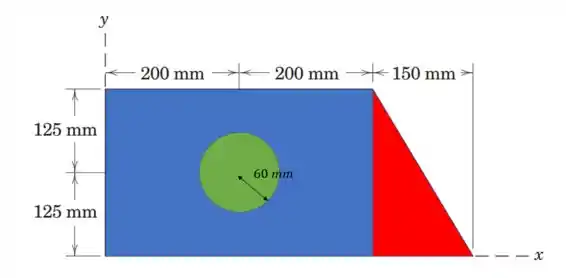
Mas atenção, o circulo em verde é uma subtração da figura, então tudo que fizermos em relação a ele tem valor negativo.
Passo 2
Vamos começar com o retângulo. Sua área é:
Agora vamos determinar o centroide desse retângulo
Passo 3
Agora vamos para o triângulo. Começando por sua área:
Vamos mudar o nosso centro do sistema de coordenadas para facilitar as contas
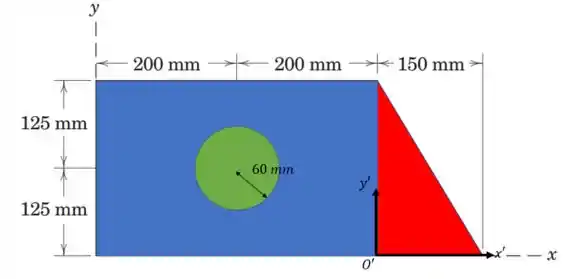
A gente colocou agora o centro em
Então temos
Agora vamos passar para as coordenadas normais.
Então
E
Passo 4
Agora só falta o círculo. A área dele fica o seguinte
Agora vamos encontrar o centroide desse círculo, e podemos fazer isso sem fazer nenhuma conta. O centroide do círculo vai ser exatamente no centro dele, e coincidentemente o centro do círculo está no mesmo ponto que o centro do retângulo, então seu centroide é
Lembrando sempre que tudo que se refere ao círculo é negativo, já que o círculo é uma parte que falta na imagem.
Passo 5
Só falta calcular o centroide da figura toda agora.
Isso fica
Substituindo esses valores
E agora para
Isso fica
Substituindo esses valores