Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 33

Se a distância h foi escolhida de modo a maximizar y - , mostre que y - = 2 h 3 .

Passo 1

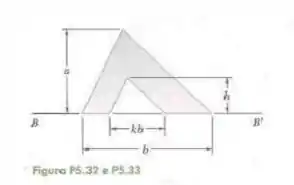
Fala aí galera, vamos pra mais um problema de estática. Vamos primeiro calcular o centroide em termos dos elementos fornecidos. Logo:

A × y - t r i â n g u l o   m a i o r = a 3 × a b 2 = a 2 b 6

A × y - t r i â n g u l o   m e n o r = h 3 × k h b 2 = k b h ² 6

Logo, o centroide será:

y - = a 2 b - k b h 2 6 a b - k h b 2 = a 2 b - k b h 2 3 a b - k h b

Para achar o máximo valor do centroide, basta derivar em relação a h   e igualar a 0:

d y - d h = - 2 k b h ( 3 a b - k h b ) - - 3 k b ( a 2 b - k b h 2 ) 3 a b - k h b 2 = 0

- 2 k b h 3 a b - k h b - - 3 k b a 2 b - k b h 2 = 0

3 k b h 2 - 6 a b h + 3 a 2 b = 0

Chegamos a uma equação de segundo grau, logo:

∆ = 36 a 2 b 2 - 36 a ² b ² k

h = 6 a b ± 6 a b 1 - k 6 k b

h = a ± a 1 - k k

Como queremos a maior distância de BB’ até o centroide, usaremos k = 0,1 :

h = 0,513 a

Logo, basta substituir na expressão do centroide:

y - = ( a 2 b - 0,1 b × 0,263 a ² )   3 a b - 0,1 × 0,513 a b = 0,9737 a 2,846

y - = 0,342 a ≈ 2 h 3

Logo, mostramos o que o problema pediu.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o suporte de batente mostrado na figura, determine a coordenadora x do centro de gravidade.
Determine o centroide das áreas planas a seguir.
Determine o centroide das áreas planas a seguir.
Localize o centroide da área plana mostrada
Localize o centroide x - da área sombreada.