Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 55
5/55) A oscilação angular da haste ranhurada é realizada pela manivela , que gira no sentido horário na velocidade constante . Determine uma expressão para a velocidade angular da haste ranhurada em termos de .
Passo 1
Vamos começar bem devagarinho, primeiro vamos entender que a velocidade angular é definida dessa forma porque é a derivada do ângulo no tempo!
Entendido isso a gente pode começar a olhar a figura e aplicar a geometria.
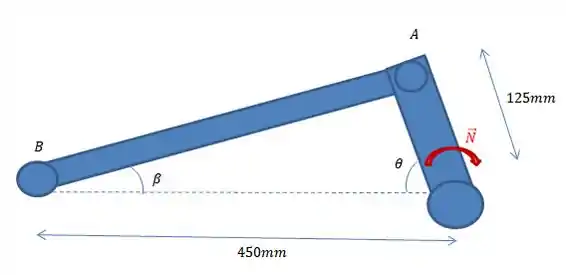
Na nossa figura, temos o nosso ângulo , o ângulo e a velocidade da manivela .
Vamos a partir dessa figura encontrar alguma relação para esse ângulo !
Passo 2
Galera , analisando a figura do problema , temos um triângulo :
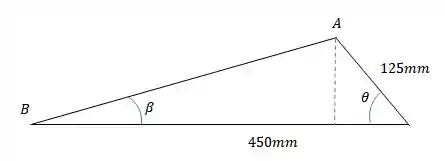
Para encontrar uma relação para o ângulo , uma boa opção é dividir esse triângulo em dois triângulos retângulos, que vão ficar com essa cara:
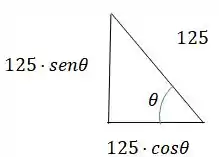
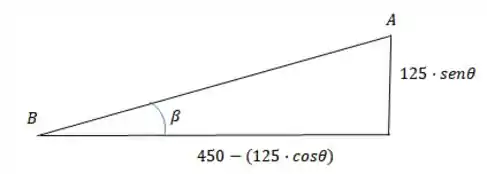
Agora que temos um triângulo retângulo com o ângulo , podemos aplicar a tangente nele!
Passo 3
A velocidade angular da haste , por sua vez , é dada por :
Essa formulinha é muito útil quando a gente quer calcular velocidade angular a partir da rotação , dada em rpm.
Passo 4
Agora vamos derivar a relação que achamos no passo 1 para obtermos
Lembrando da regra do quociente:
Sendo
e
E é importante lembrar também a seguinte derivada:
Assim:
Sendo assim ,
Passo 5
Bom pessoal , além disso , pelar relações trigonométricas básicas:
E lembrando que:
A gente vai poder obter:
Então ,
Pronto, temos em função apenas de .
obs: Gente, essa equação pode ser desenvolvida ainda mais, porém será apenas algebrismo e propriedade trigonométria.