Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 67

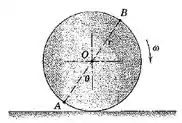
5/67) A roda de raio r rola sem deslizar e possui uma velocidade angular ω . Escreva uma expressão para a velocidade do ponto A em termos de θ e mostre que as velocidades de A e B são perpendiculares uma a outra.

Passo 1

Então galera, como aprendido neste capítulo, sabemos que nos foi dado alguns dados

Raio da roda r

Velocidade angular da roda ω

Ângulo θ

Pra facilitar a compreenção do exercicio e sempre bom que iniciemos ele com o D.C.L ok?

Então bora

Agora sim, podemos dar sequência na resolução...

Let´s boraaaaaa

Passo 2

Bom, sabemos que

v O = | v A / O | = ω r

Portanto sabemos então que v A é o resultado de v O &   v A / O

Seguindo nessa afirmação:

v A = v O 2 + v A / O 2 + 2 v O v A / O cos ⁡ ( 180 - 0 )  

v A = ω r 2 + ω r 2 + 2 ω r ω r cos ⁡ ( 180 - 0 )

v A = 2 ω r 2 - 2 ω r 2 cos ⁡ θ

v A = ω r 2 - 2 cos ⁡ θ

v A = 2 ω r 1 - cos ⁡ θ

v A = 2 ω r 2 sin 2 ⁡ θ 2

d e s d e   q u e   1 - cos ⁡ θ = 2 sin 2 ⁡ θ 2

v A = 2 ω r × 2 sin ⁡ θ 2

v A = 2 ω r sin ⁡ θ 2

Portanto, a velocidade no ponto A, é de

v A = 2 ω r sin ⁡ θ 2

Como o ângulo seria de π e a fórmula nos dá uma defasagem de θ 2 , o ângulo entre v A e v B é 90 ° .

Passo 3

v A faz um ângulo ( 90 - θ / 2 ) com v O

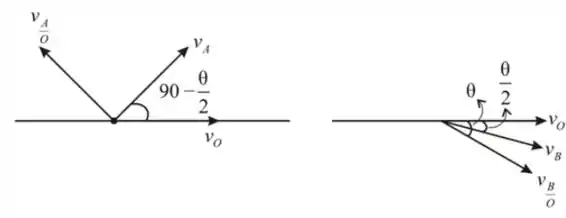
Portanto, o ângulo entre v A &   v B   é   90 °

Portantom, são perpendiculares.

Resposta

v A = 2 r ω sen ⁡ θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5/80) Os componentes de uma caçamba de mandíbulas simplificada para uma draga são apresentados . O cabo que abre e fecha a caçamba passa através do bloco em O . Com O como um ponto fixo , determine a
5/81) A extremidade A da barra possui uma velocidade para baixo v A de 2m / s durante um intervalo de seu movimento . Para a posição em que θ = 30 ° determine a velocidade angular ω de A B e a velocid
5/79) Determine a velocidade angular da barra B C para o instante indicado . No caso (a) , o centro O do disco está em um mancal fixo , enquanto no caso (b) , o disco rola sem deslizar sobre a superfí
5/74) O pino no braço rotativo O A se acopla na haste ranhurada e faz com que ela gire . Mostre que a velocidade angular de C B é a metade daquela de O A independentemente do ângulo θ .
5/78) A rotação da engrenagem é controlada pelo movimento horizontal da extremidade A da cremalheira A B . Se a haste do pistão possui uma velocidade constante x ' = 300m m / s durante um curto interv