Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 79
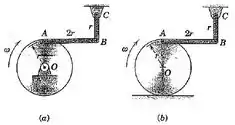
5/79) Determine a velocidade angular da barra para o instante indicado . No caso (a) , o centro do disco está em um mancal fixo , enquanto no caso (b) , o disco rola sem deslizar sobre a superfície horizontal . Em ambos os casos , o disco possui uma velocidade angular no sentido horário . Despreze a pequena distância do pino até a borda do disco .
Passo 1
Então galera , reparem que na primeira situação , temos que :
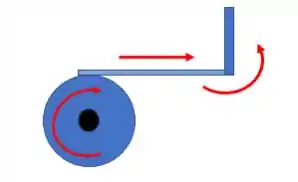
Ou seja, quando o disco gira no sentido horário o mesmo empurra a barra horizontal, que faz com que a barra gire no sentido anti-horário.
Além disso, por ser uma barra rígida, a velocidade do ponto é a mesma do ponto .
E, pro fim, a velocidade do ponto pode ser obtida através da velocidade angular do disco:
E:
Como o comprimento da barra vale , para acharmos a velocidade angular , basta aplicarmos a relação :
Passo 2
Nesse segundo caso, temos o caso de uma translação de um corpo girante. Bem, uma translaçãode um corpo girante pode ser considerada como a superposição de uma translação e de uma rotação. Tudo ocorre de forma que o ponto mais próximo do solo tenha velocidade nula (afinal de contas, o corpo rola sem deslizar) e possui duas vezes a velocidade de rotação no ponto mais alto. Como? Dá uma olhada na figura:
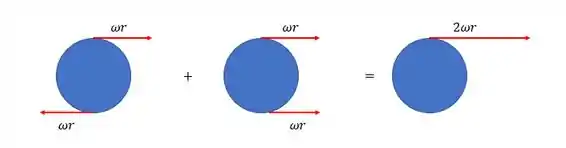
Assim:
Seguindo a mesma lógica do item anterior, a barra vai girar no sentido anti-horário e o valor de sua velocidade angular vale: