Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 121
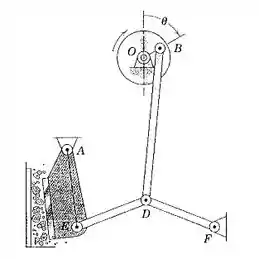
Determine a velocidade angular do aríete AE do triturador de pedras na posição em que . A manivela OB possui uma taxa de velocidade angular de 60 rpm. Quando B está na parte mais baixa do seu círculo, D e E estão em uma linha horizontal através de F, e as linhas BD e AE estão verticais. As dimensões seção , , . Trace cuidadosamente a configuração gráfica, e utilize o método dessa seção.
Passo 1
Pessoal, como o enunciado pede para traçar o diagrama com cuidado, é possível que seja necessário utilizar régua e escala para encontrar alguns dados.
Mas primeiro vamos organizar os dados da questão em forma de um diagrama.
De mais imediato, podemos converter a velocidade angular para o SI e calcular a velocidade de B:
Passo 2
Nesta etapa, vamos usar o conceito de Centro Instantâneo de Velocidade Nula C.
Sabemos que o centro instantâneo C de pontos pertencentes a um mesmo corpo pode ser encontrado traçando linhas perpendiculares aos vetores velocidade. Aonde estas linhas se encontrarem é o centro C.
Deste modo, vamos traçar linhas perpendiculares aos vetores velocidade dos pontos B, D e E Como todos estes pontos estão em corpos em um ponto articulado, seus vetores velocidade estão perpendiculares a OB, DF e AE, respectivamente.
Para descobrir os valores dos segmentos vamos utilizar a régua para medir e a escala para converter as medições. Com isto, temos que:
Passo 3
Agora, vamos calcular as velocidades. Pela haste BD, temos:
Pela haste DE, temos:
E finalmente, podemos calcular a velocidade angular