Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 120
No projeto desse mecanismo, o movimento ascendente do êmbolo G controla o movimento de uma vara de controle presa em A. O ponto B da haste AH está confinado a se deslocar com o curso deslizante sobre o eixo vertical fixo ED. Se G possui uma velocidade durante um curto intervalo, determine a velocidade de A para a posição
Passo 1
Pessoal, primeiro vamos organizar os dados da questão.
O ponto B da haste AH desliza na vertical pela haste ED, portanto, seu vetor velocidade está na vertical.
Sabemos pelo enunciado que no sentido para cima. O ponto F pertence à haste DF, que é fixa e gira no ponto D. Então, o vetor velocidade linear é perpendicular a DF. Além do mais, G e F se movimentam na vertical com a mesma velocidade. Portanto, podemos encontrar o módulo de projetando a velocidade na direção vertical e igualando a .
Com esses dados, vamos fazer um esboço do mecanismo para visualizar o problema.
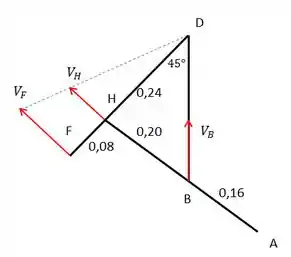
Sabendo ·, podemos calcular a velocidade angular da haste DF.
Além disso, também sabemos também a velocidade do ponto H,
Passo 2
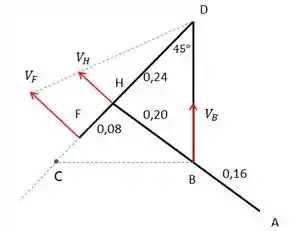
Nesta etapa, vamos usar o conceito de Centro Instantâneo de Velocidade Nula C.
Sabemos que o centro instantâneo C de pontos pertencentes a um mesmo corpo pode ser encontrado traçando linhas perpendiculares aos vetores velocidade. Aonde estas linhas se encontrarem é o centro C.
Deste modo, vamos traçar linhas perpendiculares aos vetores velocidade dos pontos H e B, pertencentes à haste AH para encontrar o centro instantâneo C.
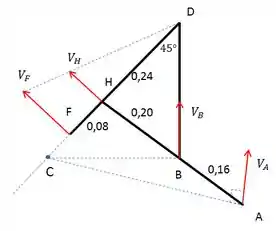
Encontrado o centro instantâneo C, podemos encontrar o vetor velocidade usando o mesmo método.
Passo 3
Agora, vamos estabelecer algumas relações geométricas para encontrar a distância CA, de modo a ser possível calcular Acompanhe a Figura junto aos cálculos abaixo.
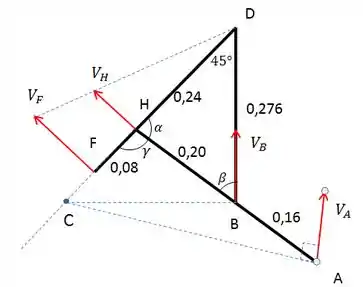
Do triângulo BDH, usamos a lei dos Senos para encontrar os valore de
Pelo triangulo, sabemos que:
E calculamos BD:
Pelo triângulo retângulo CGD, podemos calcular a distancia CD:
Agora, vamos olhar para o triangulo CHA:
Podemos encontrar gama por:
Pela lei dos Cossenos, calculamos CA:
E depois de muita geometria, enfim calculamos a velocidade de A: