Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 77

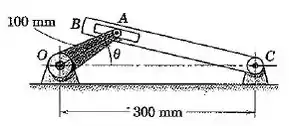
5/77) A manivela oscila em torno da posição obrigando , por sua vez , a oscilar . Se possui uma velocidade angular no sentido anti-horário de quando , determine a velocidade angular correspondente de para esse instante .

Passo 1

Falaa! Então, vamos usar nossos conhecimentos de velocidade relativa para resolver essa. Antes, vamos fazer uma figurinha para ajudar a gente nos cálculos:

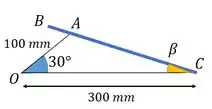
A ideia é que a gente sabe a velocidade angular em para o instante dado e quer descobrir a velocidade angular em .

E aí uma forma de achar o que ele pede, é achar a velocidade em . Aí a gente acha a velocidade angular pela fórmulinha:

Bora tentar fazer isso. Vem comigo!

Passo 2

Nesse tipo de questão com dois mecanismos, vamos começar posicionando um ponto que está na barra mas coincide com .

Vamos fazer um esqueminha de como ficaram esses vetores. é a velocidade perpendicular a barra (por isso a gente pode usar aquela fórmula com a velocidade angular) e é perpendicular a (para gente poder usar a formulinha da velocidade angular de novo hehe).

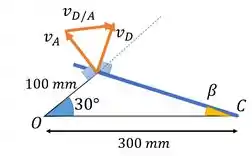
Aí a velocidade em é dada por :

Onde é a velocidade angular do eixo , e a distância da origem até :

Passo 3

Agora a gente precisa achar . Vamos ter que achar as orientações desses nossos vetores.

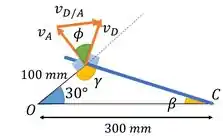
Vamos achar , para depois :

Analisando a trigonometria do triângulo indicado na figura , achamos que :

E daí, pela soma de ângulos em :

Aí esses vetores ficam assim:

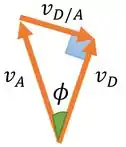
Uma observação bem importante: pela definição de velocidade relativa, para esse caso onde e coincidem, temos que o ângulo entre e é de . (só lembrar que são as duas setinhas que apontam para o mesmo lugar). Aí precisamos levar isso em consideração aqui.