Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 16
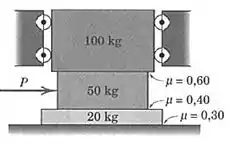
6/16) Determine a força horizontal necessária para causar deslizamento . Os coeficientes de atrito para os três pares de superfícies em contato estão indicados . O bloco superior é livre para se mover verticalmente .
Passo 1
Então pessoal , primeiro bora definir os conceitos deste problema:
Seja o peso do bloco de , o peso do bloco de e o peso do bloco de .
Para este exercícios nós temos duas possibilidades :
O bloco do meio se move e o bloco de baixo não , sendo assim :
Aplicando a equação de equilíbrio , temos que :
Logo ,
Reparem que multiplicamos por , pois a força necessária para sustentar o bloco de é afetada pelo bloco de que está sobre ele .
Passo 2
Bom galera , agora precisamos analisar a outra possibilidade :
O bloco do meio se move com o de baixo :
Aplicando a equação de equilíbrio , temos que :
Logo ,
Reparem que multiplicamos por , pois a força necessária para sustentar o bloco de é afetada pelo blocos de e que estão sobre ele .
Resposta
Respectivamente :
Tranquilo pessoal? Então partiu resolver mais questões