Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 19
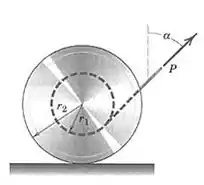
6/19) A roda mostrada rolará para a esquerda quando o ângulo for pequeno . Quando for grande , a rola rolará para a direita . Determine , por inspeção da geometria do diagrama de corpo livre , o ângulo para o qual a roda não rolará . Se o coeficiente de atrito estático é e a massa da roda , determine o valor de para o qual a roda girará para o valor crítico de .
Passo 1
Bom pessoal , pelos princípios do somatório das forças concorrentes , sabemos que as forças devem ser concorrentes para que haja equilibrio . Dessa forma :
Agora aplicando as equações de equilíbrio em relação aos eixos , obtemos que :
:
:
Passo 2
Combinando as equações e liminando , obtemos que :
Substituindo os valores que já conhecemos :
Resposta
Suave galera? Então bora próxima!!!
Exercícios de Livros Relacionados
Os coeficientes de atrito estático e cinético entre o tambor e a barra de freio são μ s = 0,4 e μ k = 0,3 , respectivamente. Se M = 50N ⋅ m e P = 85N , determine as componentes horizontal e vertical d
O menino de 40k g está sobre a viga e puxa a corda com uma força de 200N . Se μ s D = 0,4 , determine a força de atrito entre seus sapatos e a viga e as reações em A e B . A viga é uniforme e tem um p
O coeficiente de atrito estático entre o tambor e a barra de freio é μ s = 0,4 . Se M = 35N ⋅ m determine a menor força P que precisa ser aplicada à barra de freio a fim de impedir que o tambor gire.
O cone tem um peso W e centro de gravidade em G . Se uma força horizontal P for gradualmente aplicada à corda presa ao seu vértice, determine o coeficiente de atrito estático máximo para que haja desl
Resolva o problema anterior considerando que a caminhonete e a caixa estão subindo por um aclive de 10° .