Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 2

8.2. Determine a força P mínima exigida para empurrar a caixa deslize plano acima. A caixa tem massa de 50   k g e o coeficiente de atrito entre a caixa e o plano é μ s = 0,25

Passo 1

Vamos começar desenhando o diagrama de corpo livre.

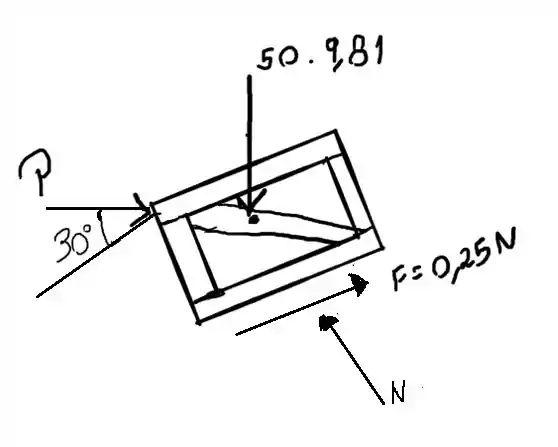
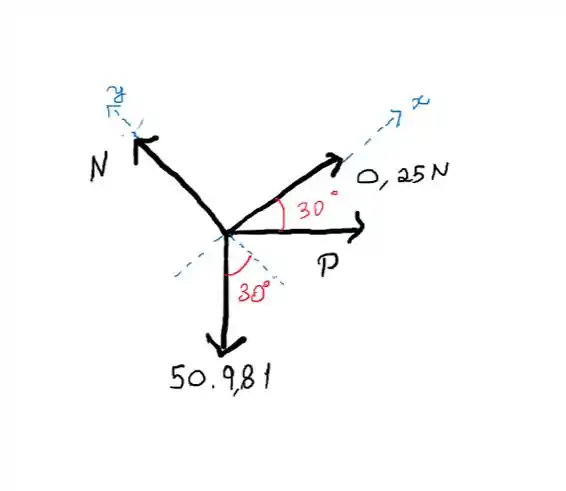
Passo 2

Agora vamos usar as equações de equilíbrio

F R y = 0

F R y = N - P ⋅ sin ⁡ 30 ° - 50 ⋅ 9,81 ⋅ cos ⁡ 30 ° = 0

E para o eixo x

F R x = 0

F R x = P ⋅ cos ⁡ 30 ° - 0,25 ⋅ N - 50 ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Passo 3

Agora temos duas equações

N - P ⋅ sin ⁡ 30 ° - 50 ⋅ 9,81 ⋅ cos ⁡ 30 ° = 0     1

P ⋅ cos ⁡ 30 ° - 0,25 ⋅ N - 50 ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0     ( 2 )

E duas incógnitas

N   e   P

Isolando N em (1)

N = P ⋅ sin ⁡ 30 ° + 50 ⋅ 9,81 ⋅ cos ⁡ 30 °

Substituindo em (2)

P ⋅ cos ⁡ 30 ° - 0,25 ⋅ ( P ⋅ sin ⁡ 30 ° + 50 ⋅ 9,81 ⋅ cos ⁡ 30 ° ) - 50 ⋅ 9,81 ⋅ sin ⁡ 30 ° = 0

Isolando P

P ⋅ cos ⁡ 30 ° - 0,25 ⋅ sin ⁡ 30 ° = 50 ⋅ 9,81 ⋅ sin ⁡ 30 ° + 0,25 ⋅ 50 ⋅ 9,81 ⋅ cos ⁡ 30 °

P = 50 ⋅ 9,81 ⋅ sin ⁡ 30 ° + 0,25 ⋅ cos ⁡ 30 ° cos ⁡ 30 ° - 0,25 ⋅ sin ⁡ 30 ° = 474,27   N

Então

N = 474,27   ⋅ sin ⁡ 30 ° + 50 ⋅ 9,81 ⋅ cos ⁡ 30 ° = 661,92   N

Resposta

P = 474,27   N N = 661,92   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois blocos A e B têm peso de 50N e 30N , respectivamente. Eles estão apoiados no planos inclinado para qual os coeficientes de atrito estático são μ A = 0,15 e μ B = 0,25 . Determine o ângulo que cau
Determine a força mínima P necessária para empurrar os dois cilindros de 75k g aclive anterior. A força atua paralelamente ao plano e os coeficientes de atrito estático das superfícies de contato são
O trator tem um peso de 40k N com centro de gravidade em G . Determine se ele pode empurrar uma tora de 250k g aclive acima. O coeficiente de atrito estático entre a tora e solo é μ s = 0,5 , e entre
O trator tem um peso de 40k N com centro de gravidade em G . Determine o maior peso dá tora que pode ser empurrado aclive acima. O coeficiente de atrito estático entre a tora e solo é μ s = 0,5 , e en
Se os coeficientes de atrito estático nos pontos de contato A e B são μ s = 0,4 e μ s ' = 0,2 , respectivamente, determine a menor força P que fará com que o carrretel de 150k g tenha iminência de mov