Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 10
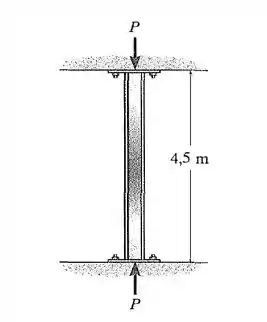
10. O elemento estrutural é feito de aço e usado como uma coluna de de comprimento. Se considerarmos que suas extremidades estão apoiadas por pinos e que ela é submetida a uma carga axial de, determine o fator de segurança em relação à flambagem.
Passo 1
Fala aí! Mas vamos refletir: O fator se segurança é um cara que a gente divide pela carga crítica para achar uma nova carga menor (que não cause flambagem) e assim admissível para a nossa coluna, assim:
A gente precisa achar esse cara para a nossa situação.
Bem! Como as extremidades da coluna estão apoiadas com pinos, de cara já tiramos que o seu fator de comprimento efetivo é igual a .
Agora, vamos tratar de obter o momento de inércia em relação ao eixo da seção transversal da nossa coluna. Porque é ele o menor. Ou seja, é por esse eixo que pode ocorrer a flambagem.
O elemento estrutural possui as seguintes propriedades:
Pronto! Já sabemos o momento de inércia em relação ao eixo .
Passo 2
Vamos então, usar a fórmula da carga crítica para a flambagem:
E substituindo os valores numéricos pertencentes a cada variável, chegamos até:
A seguir, vamos ver se há escoamento devido a essa carga, ou a coluna fica bem.
Passo 3
Agora que já sabemos o valor da carga crítica , apliquemos então a outra velha e conhecida fórmula de tensão, dada pela divisão da força pela área em que ela atua:
Esse valor é maior do que a tensão admissível para o nosso aço , que é igual a Logo, não está tudo certo com nosso resultado. E a nossa coluna não suportará a carga. Ela sairá do regime linear elástico pois ultrapassamos a tensão admissível.
Logo, a gente não pode usar como carga crítica para a nossa coluna.
Passo 4
Precisamos descobrir a carga crítica para que a gente não ultrapasse a tensão de escoamento, de acordo com a tensão admissível do aço, igual a .
Então essa vai ser a carga crítica que a gente vai considerar, tá bem? A outra a gente descarta porque ela causava escoamento do nosso material.
Passo 5
Lembra que temos essa relação:
A nossa carga crítica mudou, então vamos atualizar isso aí:
Cara, e quem é ? Ele diz que nossa coluna sofre . Como ele quer o FS para essa situação, essa carga pode ser a nossa carga admissível.
Agora, para encontrar nosso fator de segurança, basta dividir o valor da nossa carga crítica ideal (aquela em função da tensão admissível do aço) pela carga axial a que ela está sendo submetida.