Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 1
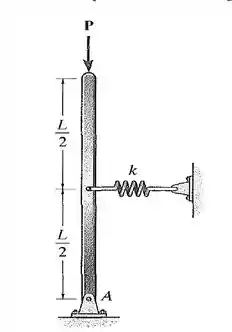
1. Determine a carga de flambagem crítica para a coluna. Podemos considerar que o material é rígido.
Passo 1
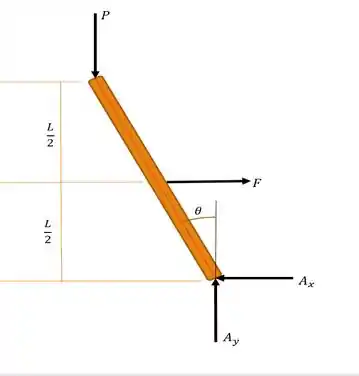
Primeiramente, vamos fazer um esboço das forças que estão agindo no nosso sisteminha, quando ela está inclinado de um ângulo devido a ação da força .
Passo 2
Viu só! A força faz com que a coluna se desloque de um ângulo no sentido anti-horário. Vamos então aplicar o somatório das forças e momentos em um ponto de nosso interesse. Que tal o ponto descrito na figura do enunciado! Não vamos nos esquececer, é claro, de que em situações de flambagem,
Aplicando o somatório das forças no ponto , numa situação em que a barra está em estado iminente de flambagem, temos que:
Antes de aplicar o somatório das forças na direção , vamos fazer duas ressalvas. A primeira é que a reação , na verdade, é igual a zero, e a segunda é que a nossa força , é uma força elástica. Logo, aplicando o somatório das forças no nosso ponto, chegamos ao seguinte resultado:
Só que o deslocamento da força elástica, nada mais é do que o comprimento flambado da coluna. De modo que nossa relação vai ter a seguinte cara:
Passo 3
Como já obtemos o valor da força no , basta agora usar a definição do valor intermediário da carga de flambagem crítica , igual a: