Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 21
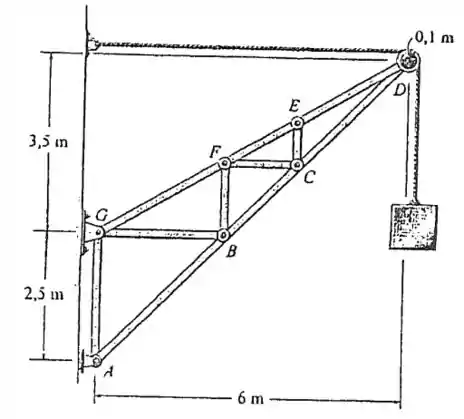
6.21 Determine a maior massa do bloco suspenso de modo que a força em qualquer membro da treliça não exceda ou
Passo 1
Fala ai galerinha bonita, tudo beleza?!
Saca só, o enuciado deu pra gente um sistema de treliças com uma apoio sistentando um bloco através de uma corda, e dado o sistema, o enunciado pede pra gente encontrar o valor máximo para a massa do bloco de modo que a força em qualquer membro da treliça não exceda (tração) ou (compressão).
Vamos usar o método dos nós abordado no começo do capitulo.
Precisamos fazer o diagrama de corpo livre para o ponto :
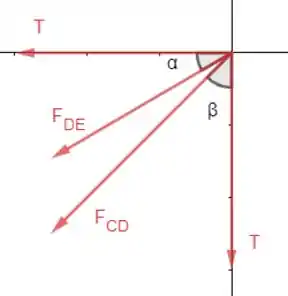
Podemos calcular os ângulos usando relações trigonométricas:
E:
Passo 2
Vamos montar as equações para e para , o somatório das forças em cada eixo deve ser igual a zero.
E do mesmo modo no eixo :
Diminuindo a segunda equação da primeira, obtemos:
Como, :
Então a equação fica:
Com o valor de podemos encontrar , vamos usar a primeira equação:
Logo:
Portanto:
O sinal negativo indica que adotamos a direção errada para o vetor , portanto essa força não está tracionando o membro CD, como está desenhado, ela é uma força de compressão.
Passo 3
Como , se olharmos para o nó vamos observar que
Como , se olharmos para o nó , vamos ver que:
e para manter o equilíbrio:
Olhado para :
Olhando para
da mesma forma que em , para manter o equilibrio:
Passo 4
Para terminar a analise, vamos fazer o diagrama de corpo livre para o nó , pois ainda precisamos descobrir a força que atua no mebro AG. Perceba que o apoio desse nó não realiza força na vertical, somente na horizontal, então:
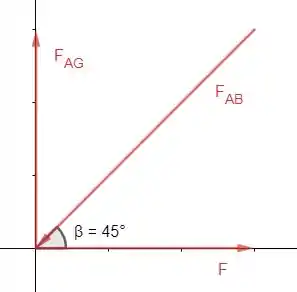
Onde é a força que a parede faz sobre o nó A.
Passo 5
O somatório de forças em e em é igual a zero, como só precisamos de vamos montar a equação só para :
E como está no diagrama essa é uma força de tração.
Passo 6
Agora precisamos descobrir o valor da massa do bloco.
A máxima, e única, tração sofrida nessa treliça é no membro AG, como a máxima tração deve ser de , escrevemos assim
Tal que:
Já a máxima compressão, que deve ser de , ocorre nos membros AB, BC e CD e valem:
Logo:
Então a maior massa do bloco que não excede os limites dados é: