Determine as forças nos elementos e da treliça carregada.
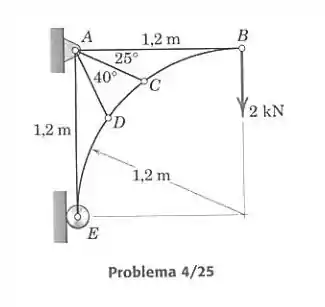
Passo 1
Vamos resolver as equações de equilíbrio no eixo e no eixo para cada nó. T determinará que a força no elemento é de tração e C que é de compressão. Nas equações, consideraremos todas de tração, tendo sinal negativo as que são de compressão.
Passo 2
Para fazer as equações para o nó B, primeiro precisamos descobrir o ângulo entre e a horizontal. Se Posicionarmos a origem no centro do círculo que tem o arco , com a coordenada apontada para a direita e para cima, teremos a equação do círculo com centro em e raio :
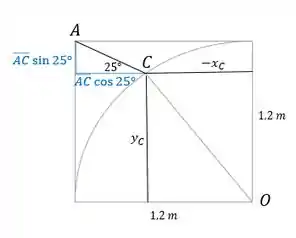
Como vemos na figura, também podemos relacionar o tamanho com e . Chamando de , temos:
Então podemos fazer:
Abrindo os quadrados:
Sabemos que . Substituindo o seno e cosseno:
Resolvendo a equação de segundo grau encontramos :
Agora conseguimos achar , da seguinte maneira:
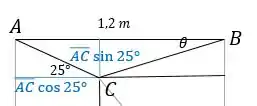
Pronto, agora como temos podemos calcular as forças para o nó .
Passo 3
Temos a seguinte configuração de forças:
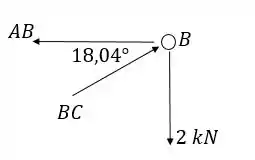
Fazendo a equação de forças em encontramos , que é de compressão:
Passo 4
Agora que temos , podemos ir para o nó C para encontrar :
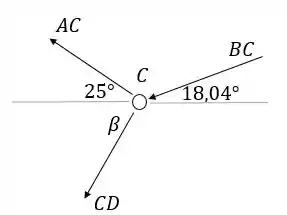
Precisamos saber quem é esse ângulo . Olhando o triângulo , que é isósceles, achamos o ângulo:
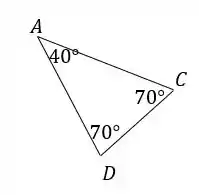
Passo 5
Fazemos então as equações de equilíbrio em :
Substituindo os senos e o valor de :
Isolamos para substituirmos na próxima equação:
Substituindo os senos e o valor de e encontrado anteriormente:
O valor negativo indica que erramos o sentido e a força é na verdade de compressão. Agora, pela simetria que há entre e no nó A: