Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 63
63. Determine a velocidade do centro de gravidade G da hiela no instante mostrado. O pistao P está se deslocando para cima com uma velocidade de 7,5 m/s.
Passo 1
Um esboço que pode ajudar na resolução do problema pode ser representado por:
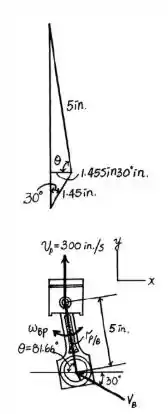
Passo 2
Da geometria, temos que:
Passo 3
De BP temos que:
Substituindo os valores acima nesta equação encontramos que:
Passo 4
Logo:
Substituindo esses valores nesta equação, encontramos que:
Resposta
Exercícios de Livros Relacionados
Um fio homogêneo de comprimento V é dobrado como mostrado e pode oscilar em torno de um pino sem fricção em B. Denotando por τ 0 o período de pequenas oscilações quando β = 0, determine o ângulo β par
Uma placa uniforme de 1,8 kg na forma de um triângulo equilátero é suspensa em seu centro de gravidade por um fio de aço que é conhecido por ter uma constante torcional K = 35 mN. m / rad. Se a placa
Um disco circular de raio r = 0,8 m está suspenso em seu centro C de fios AB e BC soldados juntos em B. As constantes de mola de torção dos fios são = 100 N m / rad para AB e K2 = 50 N . m / rad para
Um disco uniforme de raio r = 120 mm é soldado em seu centro a duas hastes elásticas de igual comprimento com extremidades fixas em A e B. Sabendo que o disco gira em um ângulo de 8 ° quando um par de
Um colar A de 1,8 kg é preso a uma mola de 800 N / in constantes e pode deslizar sem atrito em uma haste horizontal. Se o colar for movido 70 mm para a esquerda de sua posição de equilíbrio e liberado