Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas - Ex. 60
64. Localize o centroide da área da seção transversal da viga construída.
Passo 1
Antes de tudo, vamos lembrar como se acha as coordenadas do centro de gravidade do corpo composto.
Como o enunciado no pede apenas o podemos deixar os outros de lado.
Essa questão parece um pouco assustadora, mas o primeiro passo é entendê-la e separá-la que vai ficar bem fácil. Então, para início de conversa vamos refazer o desenho de forma simplificada:
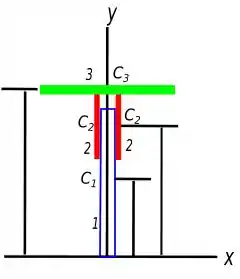
Agora que temos a imagem simplificada vamos fazer uma tabelinha semelhante a que foi feita neste capítulo para saber o que cada coisa é nos três segmentos que separamos. E a cada passo vamos completando uma parte dessa tabela:
Passo 2
Segmento 1:
Se desenharmos apenas o segmento 1 teremos essa imagem:
Assim fica simples, pois podemos ver claramente que essa parte é um retângulo, e sabemos muito bem qual é a área do retângulo. Certo?
Agora precisamos da coordenada que é a coordenada da parte do composta do corpo, ou seja, o do nosso segmento 1.
Bom, podemos ver que o nosso segmento é simétrico então o centroide se encontra exatamente no meio dele, e como só queremos o basta só usarmos a altura do segmento.
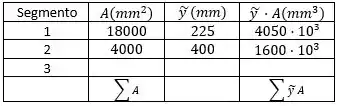
Preenchendo na nossa tabelinha teremos:
Passo 3
Segmento 2:
Desenhando apenas o segmento 2 teremos essa imagem:
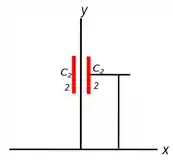
Bom, aqui precisaremos de mais atenção pois o nosso segmento está à uma certa altura do chão e essa altura vai entrar nos nossos cálculos daqui a pouco, porém vamos um passo de cada vez.
Primeiro precisaremos da área do segmento e podemos ver que as laterais se trata de dois retângulos. Na página 357 do livro podemos ler a seguinte frase “ Se um corpo composto possui um furo ou uma região geométrica sem material então considere o corpo composto sem o furo.”
O que isso nos diz? Que podemos considerar apenas os retângulos da lateral e sabemos bem como achar a área do retângulo
Porém, são dois retângulos idênticos então para achar a área é só multiplicar esse valor acima por 2.
Agora precisamos da coordenada que é a coordenada da parte do composta do corpo, ou seja, o do nosso segmento 2.
Bom, podemos ver que o nosso segmento é simétrico então o centroide se encontra exatamente no meio dele, e como só queremos o basta só usarmos a altura do segmento.
Mas só isso está certo? Não, não está!
Lembra que eu falei que o segmento está a uma certa altura do chão? Então, o centroide desse segmento também está. Como eles estão a uma altura de então o verdadeiro é:
Preenchendo na nossa tabelinha teremos:
Passo 4
Segmento 3:
Desenhando apenas o segmento 3 teremos essa imagem:
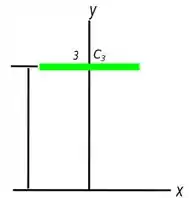
Nosso último segmento facilita bastante a nossa vida pois podemos ver claramente que essa parte é um retângulo, e sabemos muito bem qual é a área do retângulo. Certo?
Agora precisamos da coordenada que é a coordenada da parte do composta do corpo, ou seja, o do nosso segmento 3.
Bom, podemos ver que o nosso segmento é simétrico então o centroide se encontra exatamente no meio dele, e como só queremos o basta só usarmos a altura do segmento.
Mas só isso está certo? Não, não está!
Assim como o segmento anterior, o segmento 3 também está à uma certa altura do chão e essa altura vai entrar nossos cálculos. Como eles estão a uma altura de então o verdadeiro é:
Preenchendo na nossa tabelinha teremos:
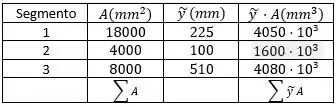
Passo 5
Agora que temos quase temos quase tudo que queremos basta fazer os somatórios necessários e aplicar na primeira formulinha lá do início.