Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 111
Calcule as reações de apoio em A e B para a viga submetida às duas distribuições de carga que variam linearmente
Passo 1
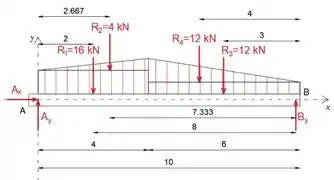
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da viga
Observe que vamos dividir a carga distribuída em 2 cargas retangulares (2-kN e 4-kN) e duas cargas triangulares (6-4 = 2kN e 6-2 = 4kN). Em seguida, substituímos as cargas distribuídas por suas resultantes atuando nos centróides.
Passo 2
Ao igualar a soma das forças na direção x a zero, podemos determinar a força de reação Ax
Ao igualar o momento sobre ponto B a zero, podemos determinar a força de reação Ay
Substitua as resultantes com os valores calculados no passo 1
Podemos expressar Ay como
Passo 3
Por fim, ao igualar a soma das forças na direção y a zero, podemos determinar a força de reação By
Substitua Ay e as resultantes por seus valores