Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 96

Calcule o volume V da grande arruela de neoprene na forma do anel completo da seção mostrada. Calcule também a área de superfície geral A.

Passo 1

Usando o teorema de Pappus, podemos escrever a expressão para a área do corpo como

A = θ ∑   x ‾ L A = θ x ‾ 1 L 1 + x ‾ 2 L 2 + x ‾ 3 L 3 + x ‾ 4 L 4                                                     ( 1 )

Onde x é o centróide das linhas, L é o comprimento das linhas e θ ângulo de rotação

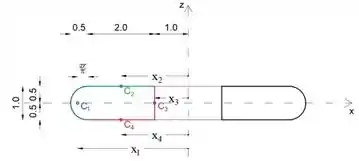
Podemos ver no esboço as seguintes dimensões:

x 1 = 1.0 + 2.0 + 2 ⋅ 0.5 π = 3.32 i n x 2 = 1.0 + 2.0 2 = 2.0 i n x 3 = 1.0 i n x 4 = 1.0 + 2.0 2 = 2.0 i n

Uma vez que os comprimentos das partes 1-3 são

L 1 = r π = 0.5 π = 1.57   i n .   L 2 = 2.0 i n L 3 = 1.0 i n L 4 = 2.0 i n

Passo 2

Uma vez que o anel está completo, o ângulo de rotação é um círculo completo.

θ = 2 π

Coloque todos os valores na expressão (1)

A = 2 π ( 3.32 ⋅ 1.57 + 2.0 ⋅ 2.0 + 1.0 ⋅ 1.0 + 2.0 ⋅ 2.0 )

A superfície total da área é A = 89.30 i n 2

Passo 3

Usando o teorema de Pappus, podemos escrever a expressão para a área do corpo como

V = θ ∑ x - A V = θ x - 1 A 1 + x - 2 A 2                                                           ( 2 )

Onde x é o centróide das linhas, A é a área e θ ângulo de rotação

Podemos ver no esboço as seguintes dimensões:

x 1 = 2.0 + 1.0 + 4 ⋅ 0.5 3 π = 3.21 i n x 2 = 1.0 + 2.0 2 = 2.0 i n

Uma vez que as áreas das partes 1-2 são

A 1 = 0.5 2 π 2 = 0.39 i n 2 A 2 = 2.0 ⋅ 1.0 = 2.0 i n 2

E o ângulo de rotação é, mais uma vez

θ = 2 π

Coloque todos os valores na expressão (2)

V = 2 π ( 3 . 21 ⋅ 0.39 + 2.0 ⋅ 2.0 )

O volume total é V = 33.00 i n 3

Resposta

A = 89.30 i n 2 V = 33.00 i n 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a distância h à qual um furo precisa ser escavado no cilindro de modo que o centro de massa do conjunto esteja localizado em x - = 64m m . O material tem uma densidade de 8M g / m 3 .
Determine a localização ( x - , y - ) do centroide para a forma estrutural. Despreze a espessura do membro.
Localize o centroide y - da área sombreada.
Localize o centroide ( x - , y - ) da área composta.
A parede de gravidade é feita de concreto. Determine a localização x - , y - do centro de massa G para a parede.