6/48) Um bloco de massa é colocado entre a parede vertical e o pequeno rolete ideal na extremidade superior , , da barra esbelta uniforme de massa . A extremidade inferior , , da barra repousa sobre asuperfície horizontal . Se o coeficiente de atrito estático em e também entre o bloco e a parede vale , determine a expressão geral para o valor mínimo , , de para o qual o bloco permaneceráem equilíbrio . Avalie sua expressão para e . Para essas condições , verifique a possibilidade de haver deslizamento em .
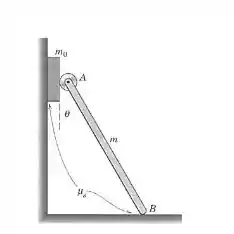
Passo 1
Então galera , a primeira coisa que devemos perceber é que nessa situação em que temos , a força de atrito entre o bloco e a parede vertical atinge seu valor máximo .
Agora devemos aplicar as equações de equilíbrio para o bloco e a barra . Temos que :
Bloco :
Logo ,
Barra :
Portanto ,
Passo 2
Bom pessoal , combinando (1) e (2) , obtemos que :
Isolando na equação , por sua vez , achamos que :
Substituindo pelos valores que já conhecemos , obtemos que :
Passo 3
Bom galera , bora checar as equações de equilíbrio da barra para , para garantirnos que não ocorre deslizamento em :
Barra :
Então ,
Logo ,
Substituindo pelos valores que já conhecemos , obtemos que :
Agora reparem que ,então não ocorre deslizamento em .
Resposta
Não ocorre deslizamento em , pois .
Suave galera? Então bora pra próxima!!!