Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 114

Sabendo que a = 100   m m , determine o máximo valor do coeficiente de atrito estático para o qual o freio é autotravante quando o tambor roda no sentido anti-horário.

Passo 1

Bom galera, começamos fazendo um diagraminha:

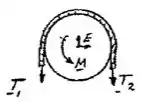
Com isso temos:

r = 200   m m

β = 180 ° = π   r a d i a n o

T 2 T 1 = e μ β = e μ π

→ T 2 = e μ π T 1

Passo 2

Show de bola, vamos analisar a barra de controle:

∑ M C = 0

→ P 0,7 - T 1 0 , 3 + T 2 0 , 1 = 0

Agora, substituindo T 2 :

→ 0,7 P - 0,3 T 1 + ( e μ π T 1 ) 0,1 = 0

Passo 3

Por fim, usando P = 0 , temos:

e μ π T 1 0,1 = 0,3 T 1

→ 0,1 e μ π T 1 = 0,3 T 1

→ 0,1 e μ π = 0,3

→ e μ π = 3

Isso é muito fácil, a gente sabe que:

μ π = ln ⁡ 3 = 1,0986

μ = 1,0986 π = 0,3497

Resposta

μ = 0,3497

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina e uniforme de comprimento l é colocada na abertura de largura d no ângulo 30∘ mostrado. Para qual intervalo de l/d a barra permanecerá em equilíbrio estático? O coeficiente de atrito está
O corpo quadrado homogêneo é posicionado conforme mostrado. Se o coeficiente de atrito estático em B for 0,40, determine o valor crítico do ângulo θ abaixo do qual ocorrerá o escorregamento. Negligenc
Repita Prob. 28/06, mas agora o carro tem tração nas quatro rodas. Suponha que o escorregamento ocorra em A e B simultaneamente.
Determine o valor máximo do ângulo θ para o qual a barra fina e uniforme permanecerá em equilíbrio. O coeficiente de atrito estático em A é μA = 0,80, e o atrito associado ao pequeno rolo em B pode se
O freio de bloco de alavanca única impede a rotação do volante sob um torque no sentido anti-horário M. Encontre a força P necessária para evitar a rotação se o coeficiente de atrito estático for μs.