Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 56
6.56. Determine a força nos elementos AB, AG e FG na treliça mostrada na figura.
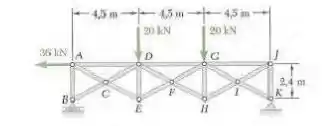
Passo 1
Vamos fazer o desenho disso
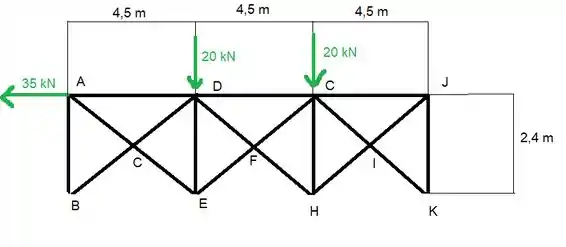
A primeira coisa que a gente pode fazer é determinar aa forças de reação em B e em K, para determinar a força de reação em B, que só vai ter componente em y, vamos usar o momento em K (aí nenhuma força de reação em K entra nessa calculo, e a gente só tem uma incógnita)
Então
Agora que a gente tem a força de reação em B, a gente pode usar o somatório das forças para determinar K
Logo
Agora em y
Logo
Passo 2
Agora a gente pode usar o método das seções para resolver o problema, vamos seccionar desse jeito:
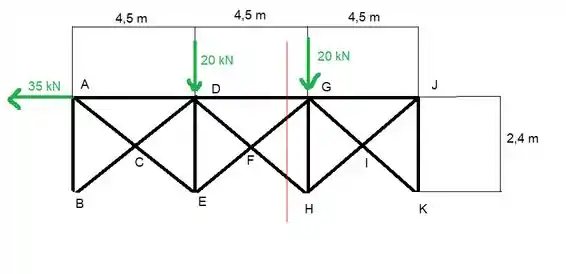
E aí a gente tem
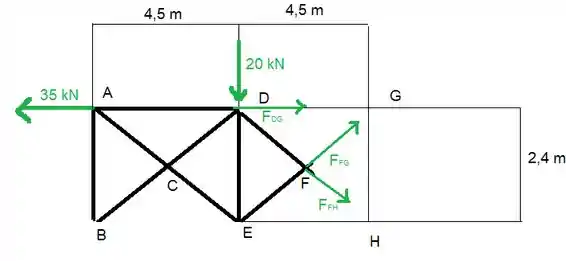
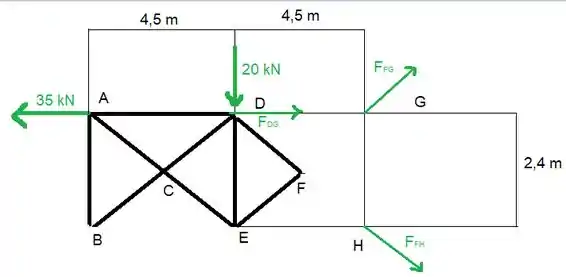
Passo 3
Beleza, agora a gente pode calcular os momentos, vamos usar o momento no ponto F. Repare que as forças, e são forças que agem no ponto F, então elas não são consideradas no momento.
Logo
Passo 4
Agora para determinar a força vamos usar o momento em D, repare que e não produzem nenhum efeito de rotação se estivermos analisando o momento em A, por tanto não vamos considerar essas forças no cálculo do momento.
Vamos calcular a componente em y da força
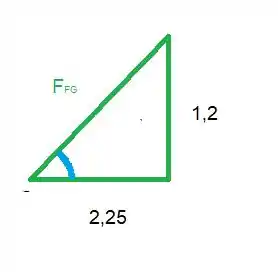
Então
Vamos fazer a hipotenusa
Então
Logo
Passo 5
Agora só falta a força , vamos usar o momento em G para calcula-la. Repare que as forças e estão agindo em G, então elas não entram no calculo do momento
Vamos decompor
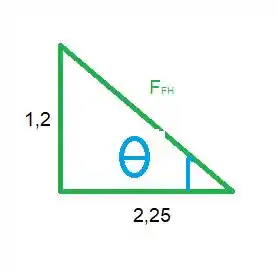
A hipotenusa é a mesma que a gente já tinha calculado. 😊
Então
Logo