Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 51
Determine as forças nos elementos , e da treliça em arco de um telhado.
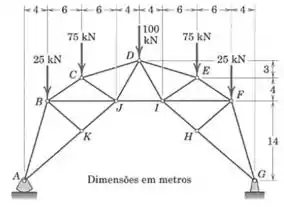
Passo 1
A força total (vinda de cima) agindo sobre a treliça é a seguinte:
E por simetria podemos garantir que essa força será dividida igualmente entre os apoios em e , ou seja:
Passo 2
Para encontrar a força , vamos aplicar o método das seções no seguinte pedaço da treliça:
Vamos encontrar expressões para esses ângulos que desenhamos:
Agora podemos começar a pensar nas forças. Vamos calcular o momento em relação ao ponto :
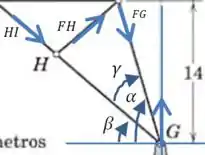
E quando fazemos o momento em relação ao ponto , ficamos apenas com a força e a força de no ponto :
E então:
Passo 3
E agora vamos mudar a seção que estamos analisando:
E agora vamos considerar primeiro o momento em relação ao ponto :
E agora o momento em relação ao ponto :
Onde o ângulo pode ser calculado pela seguinte expressão:
Passo 4
E finalmente podemos calcular a força usando a condição de equilíbrio das forças no eixo vertical para as forças nesse mesmo trecho:
Que, pelo sinal comparado ao desenho, é uma força de tração.
Resposta
As forças são (tração), (tração), (compressão), (tração).