Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 46
Os quadros articulados e estão ligados por duas barras articuladas, e , que se cruzam sem estarem interligadas. Calcule a força em .
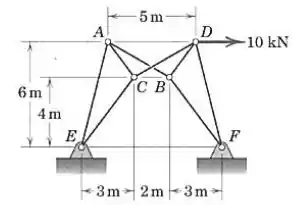
Passo 1
Vamos começar dividindo a treliça em duas partes e representando as forças externas que agem em cada uma:
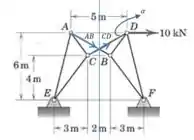
E como as forças desconhecidas estão em e , vamos montar equações de equilíbrio em torno desses pontos, dessa forma essas forças terão momento nulo.
Passo 2
Começamos com o momento em relação ao ponto , considerando apenas o lado esquerdo da linha que representamos no nosso desenho.
Perceba que o ângulo que desenhamos ali também é o ângulo que forma com a horizontal, e então o momento gerado por essa força em relação ao ponto é:
Onde basicamente separamos a força em dois componentes e calculamos o momento gerado por cada um. Agora faremos o mesmo para a força :
Agora podemos escrever o momento total em relação ao ponto :
E precisamos de uma expressão para o ângulo :
E então:
Passo 3
Agora vamos basicamente repetir a mesma conta, mas para o lado direito, e em relação ao ponto . Dessa vez temos que considerar também a força de que está representada no desenho.
E substituindo :
E agora é só pegar o resultado da equação anterior e substituir aqui:
O que está de acordo com o nosso desenho, pois é uma força de compressão.
Resposta
A força é (compressão).